 |
A B. 4548. feladat (2013. május) |
B. 4548. Adott az ABC egységnyi befogójú, egyenlő szárú derékszögű háromszög, valamint az AB oldalon az A1, a BC oldalon a B1 és a CA átfogón a C1 pont. Minimálisan mekkora lehet az A1B1 távolság, ha az ABC és az A1B1C1 háromszögek hasonlók?
Kvant
(4 pont)
A beküldési határidő 2013. június 10-én LEJÁRT.
Megoldás. Az \(\displaystyle A_1B_1C_1\) háromszög derékszögű csúcsa vagy valamelyik befogón vagy az átfogón van.
I. eset: a derékszögű csúcs az átfogón található. Ekkor az \(\displaystyle A_1BB_1C_1\) négyszög húrnégyszög, mivel szemközti szögeinek összege \(\displaystyle 180^{\circ}\) (1. ábra).
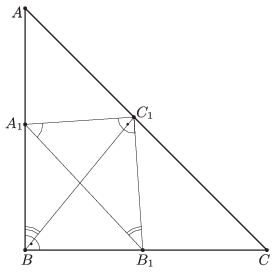
1. ábra
Az azonos húrhoz tartozó kerületi szögek egyenlők, így \(\displaystyle A_1BC_1\sphericalangle= A_1B_1C_1\sphericalangle= 45^{\circ}\), tehát az \(\displaystyle ABC\sphericalangle\)-et a \(\displaystyle BC_1\) szakasz felezi. Mivel az \(\displaystyle ABC\) háromszög egyenlő szárú, ezért ez a szögfelező egyben oldalfelező is, és így a \(\displaystyle C_1\) pont az \(\displaystyle AC\) szakasz felezőpontjában található (2. ábra).
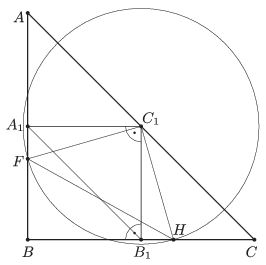
2. ábra
Legyen a \(\displaystyle B_1\) pont a \(\displaystyle BC\), az \(\displaystyle A_1\) pont pedig az \(\displaystyle AB\) oldal felezőpontja. Ekkor az \(\displaystyle A_1B_1C_1\) és az \(\displaystyle ABC\) háromszög közötti hasonlósági arány 1:2. Mivel \(\displaystyle BC=1\), ezért \(\displaystyle AC=\sqrt2\) és így \(\displaystyle A_1B_1=\frac{\sqrt2}{2}\).
Tekintsünk egy másik, \(\displaystyle C_1\) csúcsú, egyenlő szárú derékszögű háromszöget. Mivel \(\displaystyle C_1B_1\perp BC\), ezért ilyet csak úgy kapunk, ha egy \(\displaystyle C_1\) középpontú, \(\displaystyle r>C_1B_1\) sugarú körrel metsszük el az \(\displaystyle ABC\) háromszög befogóit. A kapott háromszög befogója így nagyobb lesz, mint \(\displaystyle C_1B_1\), és így nyilván az átfogója is nagyobb lesz, mint az \(\displaystyle A_1B_1C_1\) háromszögé: \(\displaystyle FH>A_1B_1\).
Tehát ebben az esetben \(\displaystyle A_1B_1\) minimuma \(\displaystyle \frac{\sqrt2}{2}\).
II. eset: a derékszögű csúcs az egyik befogón található.
Legyen \(\displaystyle A_1B_1=x\) és \(\displaystyle B_1C=y\). Ekkor \(\displaystyle A_1C_1=x\sqrt2\).
Jelölje a \(\displaystyle CB_1C_1\) szöget \(\displaystyle \alpha\). Ekkor \(\displaystyle CC_1B_1\sphericalangle= 180^{\circ}-45^{\circ}-\alpha= 135^{\circ}-\alpha\). Ebből \(\displaystyle AC_1A_1\sphericalangle= 180^{\circ}-CC_1B_1\sphericalangle- B_1C_1A_1\sphericalangle=\alpha\) és így \(\displaystyle AA_1C_1\sphericalangle=135^{\circ}-\alpha\). Tehát a \(\displaystyle B_1CC_1\triangle\) és a \(\displaystyle C_1AA_1\triangle\) a szögei egyenlőek, ezért a két háromszög hasonló. Így \(\displaystyle \frac{AC_1}{y}=\frac{x\sqrt2}{x}\), amiből \(\displaystyle AC_1=y\sqrt2\) (3. ábra).
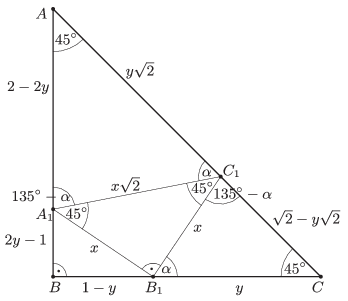
3. ábra
Mivel \(\displaystyle BC=1\), ezért egyrészt \(\displaystyle BB_1=1-y\), másrészt \(\displaystyle AC=\sqrt2\), és ebből \(\displaystyle CC_1=\sqrt2-y\sqrt2\). Tudjuk, hogy \(\displaystyle AA_1=\sqrt2 CC_1\), amiből \(\displaystyle AA_1=\sqrt2 \big(\sqrt2-y\sqrt2\,\big)=2-2y\), és így \(\displaystyle A_1B=1-(2-2y)=2y-1\).
Az \(\displaystyle A_1BB_1\) háromszögben felírhatjuk a Pitagorasz-tételt:
\(\displaystyle {(2y-1)}^2+ {(1-y)}^2=x^2, \quad\text{vagyis}\quad 5y^2-6y+2=x^2. \)
Látható, hogy \(\displaystyle x\)-nek pontosan akkor van minimuma, amikor az \(\displaystyle 5y^2-6y+2\) kifejezésnek (ha a kifejezés értéke ott pozitív). Ennek a másodfokú függvénynek a minimumhelye \(\displaystyle y=-\frac{b}{2a}=-\frac{-6}{2\cdot5}=\frac 35\)-ben van, ekkor
\(\displaystyle A_1B_1=x=\sqrt{5\cdot\left(\frac 35\right)^{\!\!2} -6\cdot\frac 35+2}=\frac{\sqrt5}{5}<\frac{\sqrt2}{2}. \)
Tehát az \(\displaystyle A_1B_1\) távolság minimálisan \(\displaystyle \frac{\sqrt5}{5}\) lehet.
Emri Tamás (Budapest, Városmajori Gimn., 11. évf.) megoldása alapján
Statisztika:
44 dolgozat érkezett. 4 pontot kapott: Balogh Menyhért, Baran Zsuzsanna, Bingler Arnold, Csépai András, Emri Tamás, Fekete Panna, Gyulai-Nagy Szuzina, Janzer Barnabás, Janzer Olivér, Katona Dániel, Khayouti Sára, Kovács 972 Márton, Makk László, Mezősi Máté, Mócsy Miklós, Nagy Gergely, Nagy-György Pál, Pap Tibor, Sagmeister Ádám, Sal Kristóf, Simkó Irén, Somogyvári Kristóf, Talyigás Gergely, Vető Bálint. 3 pontot kapott: Bereczki Zoltán, Heinc Emília, Kovács Balázs Marcell, Leitereg Miklós, Paulovics Zoltán, Szász Dániel Soma, Szőke Tamás. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2013. májusi matematika feladatai
