A B. 4627. feladat (2014. április)

B. 4627. Az \(\displaystyle ABC\) háromszög derékszögű \(\displaystyle C\) csúcsából induló szögfelező a körülírt kört a \(\displaystyle P\), az \(\displaystyle A\)-ból induló szögfelező pedig a \(\displaystyle Q\) pontban metszi. A \(\displaystyle PQ\) és \(\displaystyle AB\) szakaszok metszéspontja \(\displaystyle K\). A beírt kör középpontja \(\displaystyle O\), az \(\displaystyle AC\) oldalon levő érintési pont \(\displaystyle E\). Bizonyítsuk be, hogy az \(\displaystyle E\), \(\displaystyle O\) és \(\displaystyle K\) pontok egy egyenesbe esnek.

Javasolta: Sárosdi Zsombor (Veresegyház)

(4 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldás. Legyen \(\displaystyle CAB\sphericalangle =\alpha\), ekkor \(\displaystyle CBA\sphericalangle =\beta=90^{\circ}-\alpha\). A kerületi szögek tétele miatt:

\(\displaystyle CPA\sphericalangle =CBA\sphericalangle =90^{\circ}-\alpha, \)

hasonlóan

\(\displaystyle BAQ\sphericalangle =CAQ\sphericalangle =CPQ\sphericalangle =\frac{\alpha}{2}. \)

Így \(\displaystyle OAK\sphericalangle =OPK =\frac{\alpha}{2}\), ezért \(\displaystyle OKPA\) húrnégyszög. Az \(\displaystyle OKPA\) húrnégyszög köré írt körben \(\displaystyle OKA\sphericalangle =OPA\sphericalangle =90^{\circ}-\alpha\), mivel azonos íven nyugvó kerületi szögek.

Hosszabbítsuk meg \(\displaystyle OK\)-t, legyen \(\displaystyle OK\) és \(\displaystyle AC\) metszéspontja \(\displaystyle D\). A háromszög belső szögeinek összege \(\displaystyle 180^{\circ}\), ezért

\(\displaystyle KDA\sphericalangle =180^{\circ}-DKA\sphericalangle -DAK\sphericalangle =90^{\circ}. \)

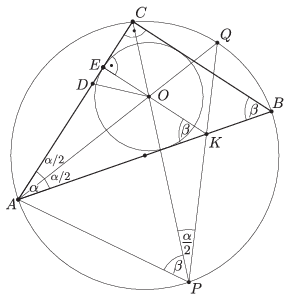
Így \(\displaystyle KDA\sphericalangle =90^{\circ}\). Az \(\displaystyle O\)-nak az \(\displaystyle AC\)-re való merőleges vetülete az \(\displaystyle E\) pont. Ebből következik, hogy \(\displaystyle D=E\), tehát \(\displaystyle E\), \(\displaystyle O\) és \(\displaystyle K\) kollineárisak.

Szebellédi Márton (Budapesti Fazekas M. Ált. Isk. és Gimn., 10. évf.) dolgozata alapján

Statisztika:

68 dolgozat érkezett.
4 pontot kapott:	57 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	4 versenyző.

A KöMaL 2014. áprilisi matematika feladatai