A B. 4677. feladat (2014. december)

B. 4677. Igazoljuk, hogy ha az $\displaystyle ABCD$ tetraéder egyenlő oldalú (azaz szemközti élei egyenlő hosszúak), akkor a $\displaystyle D$-ből induló magasságvonal talppontja rajta van az $\displaystyle ABC$ háromszög Euler-egyenesén.

Javasolta: Szabó Csaba (Budapest)

(6 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldás. A megoldás kulcsa az a tény, hogy egy egyenlő oldalú tetraéder körülírt gömbjének $\displaystyle K$ középpontja egybeesik a tetraéder $\displaystyle S$ súlypontjával.

Tekintsük az egyenlő oldalú tetraéderünk $\displaystyle AB_{1}CD_{1}A_{1}BC_{1}D$ bennfoglaló paralelepipedonját (1. ábra). Mivel a szemközti paralelogrammalapok nem megfelelő átlói egyenlők, ezért minden lapja téglalap, vagyis igazából téglatestet adtunk meg. Ekkor $\displaystyle K$ éppen a téglatest köré írt gömb középpontja, hisz ez a gömb $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$-t tartalmazza. Továbbá $\displaystyle S$ az $\displaystyle AC$ oldal $\displaystyle F$ felezőpontját ($\displaystyle AB_{1}CD_{1}$ középpontját) és a $\displaystyle BD$ oldal $\displaystyle G$ felezőpontját ($\displaystyle A_{1}BC_{1}D$ középpontját) összekötő szakasz felezőpontja. Mindkettő definíció a téglatest középpontját adja meg, ezért $\displaystyle K=S$.

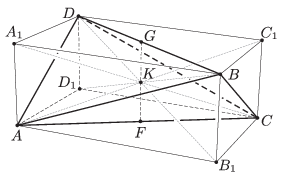
1. ábra

Legyen $\displaystyle S_{0}$ az $\displaystyle ABC$ háromszög súlypontja. A tetraéder geometriájából ismert, hogy $\displaystyle S$ a $\displaystyle DS_{0}$ súlyvonal $\displaystyle S_{0}$-hoz közelebbi negyedelőpontja. Legyen $\displaystyle K$merőleges vetülete az $\displaystyle ABC$ síkra $\displaystyle K_{0}$, akkor az $\displaystyle AK_{0}K$, $\displaystyle BK_{0}K$, $\displaystyle CK_{0}K$ háromszögek egybevágóak, hiszen derékszögű háromszögek, melyeknek átfogója ($\displaystyle r$) és $\displaystyle K_{0}K$ befogója megegyezik, emiatt $\displaystyle K_{0}A=K_{0}B=K_{0}C$, vagyis $\displaystyle K_{0}$ az $\displaystyle ABC$ háromszög köré írt kör középpontja (2. ábra).

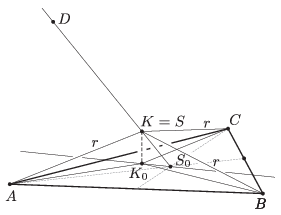
2. ábra

Tekintsük az $\displaystyle S_{0}$ középpontú 4-szeres nagyítást. Ezzel a transzformációval, mint tudjuk, $\displaystyle S$ képe $\displaystyle D$ lesz, s eközben $\displaystyle K_{0}$ (az $\displaystyle S=K$ pont vetülete az $\displaystyle ABC$ síkon) a $\displaystyle D$ pont vetületébe, $\displaystyle D_{0}$-ba képződik (3. ábra).

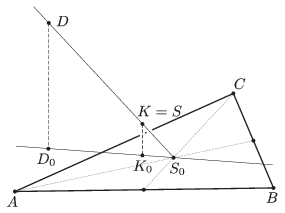
3. ábra

Ezzel megkaptuk, hogy a $\displaystyle D$ pont merőleges vetülete, vagyis a tetraéder $\displaystyle D$-ből induló magasságának talppontja az $\displaystyle ABC$ háromszög $\displaystyle S_{0}K_{0}$ Euler-vonalára illeszkedik.

Megjegyzés. A feladat kitűzése, így a megoldás is feltételezi, hogy az $\displaystyle ABC$ háromszögnek van Euler-vonala, azaz $\displaystyle S_{0}\ne K_{0}$. Ismert, hogy ez pontosan akkor áll fenn, ha $\displaystyle ABC$ háromszög nem szabályos. Vagyis a feladat állítása és a bizonyítás csakis nem szabályos, egyenlő oldalú tetraéderekre érvényes. (Szabályos tetraéderben $\displaystyle D$ vetülete $\displaystyle ABC$-re éppen $\displaystyle S_{0}{=K}_{0}$.)

Williams Kada (Szeged, Radnóti M. Kís. Gimn. és Ált. Isk., 10. évf.) dolgozata alapján

Statisztika:

35 dolgozat érkezett.
6 pontot kapott:	Andi Gabriel Brojbeanu, Andó Angelika, Baran Zsuzsanna, Bereczki Zoltán, Cseh Kristóf, Csépai András, Döbröntei Dávid Bence, Fekete Panna, Gál Boglárka, Gáspár Attila, Gyulai-Nagy Szuzina, Katona Dániel, Kovács 101 Dávid Péter, Kovács Péter Tamás, Lajkó Kálmán, Mócsy Miklós, Molnár-Sáska Zoltán, Nagy-György Pál, Porupsánszki István, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Szécsényi Nándor, Széles Katalin, Tóth Viktor, Vághy Mihály, Varga-Umbrich Eszter, Várkonyi Dorka, Wei Cong Wu, Williams Kada.
5 pontot kapott:	Keresztfalvi Bálint, Khayouti Sára.
4 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2014. decemberi matematika feladatai