A B. 4684. feladat (2015. január)

B. 4684. Az \(\displaystyle ABCD\) négyszög átlói merőlegesek egymásra, a metszéspontjuk \(\displaystyle E\). Az \(\displaystyle E\) pontból bocsássunk merőlegest mind a négy oldalegyenesre. Tekintsük mindegyik merőlegesnek a szemközti oldallal való metszéspontját. Igazoljuk, hogy ez a négy pont egy olyan körön van, amelynek középpontja az átlók felezőpontját összekötő szakaszra illeszkedik.

Javasolta: Miklós Szilárd (Herceghalom)

(5 pont)

A beküldési határidő 2015. február 10-én LEJÁRT.

Megoldásvázlat: Vegyünk fel egy \(\displaystyle (x, y)\) koordináta-rendszert, amelyben az \(\displaystyle E\) pont az origó, az \(\displaystyle AC\) oldal az \(\displaystyle x\) tengelyre, a \(\displaystyle BD\) oldal pedig az \(\displaystyle y\) tengelyre illeszkedik.

Ekkor a négyszög csúcsainak koordinátái a következők: \(\displaystyle A(a, 0)\), \(\displaystyle B(0, b)\), \(\displaystyle C(c, 0)\) és \(\displaystyle D(0, d)\), ahol \(\displaystyle a\) és \(\displaystyle b\) pozitív, \(\displaystyle c\) és \(\displaystyle d\) pedig negatív valós számok.

\(\displaystyle E\)-ből az \(\displaystyle AB\) oldalra bocsátott merőleges legyen az \(\displaystyle e\) egyenes, a \(\displaystyle BC\)-re bocsátott az \(\displaystyle f\) egyenes, a \(\displaystyle CD\)-re bocsátott a \(\displaystyle g\) egyenes, a \(\displaystyle DA\)-ra bocsátott pedig a \(\displaystyle h\) egyenes.

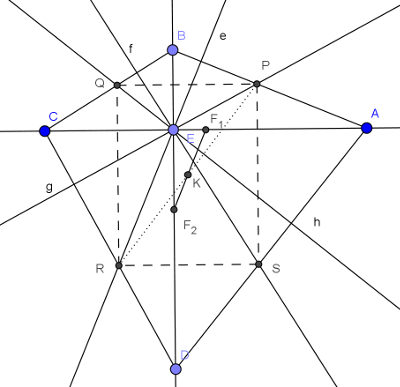
Ekkor az \(\displaystyle AB\) egyenes egyenlete: \(\displaystyle y=-\frac{b}{a}\cdot x+b\), a \(\displaystyle BC\) egyenes egyenlete: \(\displaystyle y=-\frac{b}{c}\cdot x+b\), a \(\displaystyle CD\) egyenes egyenlete: \(\displaystyle y=-\frac{d}{c}\cdot x+d\), míg a \(\displaystyle DA\) egyenes egyenlete: \(\displaystyle y=-\frac{d}{a}\cdot x+d\).

A merőlegesség miatt az \(\displaystyle e\) egyenes egyenlete: \(\displaystyle y=\frac{a}{b}\cdot x\), az \(\displaystyle f\) egyenes egyenlete: \(\displaystyle y=\frac{c}{b}\cdot x\), a \(\displaystyle g\) egyenes egyenlete: \(\displaystyle \frac{c}{d}\cdot x\), a \(\displaystyle h\) egyenes egyenlete pedig: \(\displaystyle \frac{a}{d}\cdot x\).

Az \(\displaystyle AB\) szakasz és a \(\displaystyle g\) egyenes metszéspontja legyen a \(\displaystyle P\) pont, a \(\displaystyle BC\) szakasz és a \(\displaystyle h\) egyenes metszéspontja a \(\displaystyle Q\) pont, a \(\displaystyle CD\) szakasz és az \(\displaystyle e\) egyenes metszéspontja az \(\displaystyle R\) pont, valamint a \(\displaystyle DA\) szakasz és az \(\displaystyle f\) egyenes metszéspontja az \(\displaystyle S\) pont.

Ekkor \(\displaystyle P\) első koordinátája az egyenletrendszer megoldásából:

\(\displaystyle -\frac{b}{a}\cdot x+b=\frac{c}{d}\cdot x,\)

\(\displaystyle x=\frac{bad}{bd+ac}.\)

Az \(\displaystyle S\) pont első koordinátája a megfelelő egyenletrendszerből:

\(\displaystyle -\frac{d}{a}\cdot x+d=\frac{c}{b}\cdot x,\)

\(\displaystyle x=\frac{bad}{ac+bd}.\)

Látjuk, hogy \(\displaystyle P\)-nek és \(\displaystyle S\)-nek ugyanaz az első koordinátája, vagyis a \(\displaystyle PS\) egyenes párhuzamos az \(\displaystyle y\) tengellyel.

A \(\displaystyle Q\) pont és az \(\displaystyle R\) pont \(\displaystyle x\) koordinátája hasonló számolással:

\(\displaystyle x=\frac{bcd}{ac+bd}.\)

Tehát \(\displaystyle Q\)-nak és \(\displaystyle R\)-nek is ugyanaz az \(\displaystyle x\) koordinátájuk, így \(\displaystyle QR\) is párhuzamos az \(\displaystyle y\) tengellyel.

Az eddigiek alapján már az \(\displaystyle y\) koordináták is kiszámolhatók. Például a \(\displaystyle P\) pontra:

\(\displaystyle y=\frac{bad}{bd+ac}\cdot \frac{c}{d}=\frac{bac}{bd+ac}.\)

Hasonló módon számolva a többi pontra:

\(\displaystyle Q\text{: } y=\frac{bac}{bd+ac}\), \(\displaystyle R\text{: } y=\frac{dac}{bd+ac}\), \(\displaystyle S\text{: } y=\frac{dac}{bd+ac}.\)

Beláttuk, hogy \(\displaystyle PQ\) és \(\displaystyle RS\) is párhuzamos az \(\displaystyle x\) tengellyel. A \(\displaystyle PQRS\) négyszög oldalai párhuzamosak a tengelyekkel, tehát téglalap. Annak a körnek a középpontja, amelyen ezek a pontok rajta vannak, a téglalap átlóinak metszéspontja.

Tehát már csak azt kell belátni, hogy a téglalap középpontja rajta van az \(\displaystyle AC\) és \(\displaystyle BD\) átlók felezőpontjait összekötő szakaszon.

A téglalap középpontja a \(\displaystyle K\) pont, a \(\displaystyle PR\) átló felezőpontja:

\(\displaystyle K \Big(\frac{bd(a+c)}{2(bd+ac)}, \frac{ac(b+d)}{2(bd+ac)}\Big)\)

Legyen \(\displaystyle AC\) felezőpontja az \(\displaystyle F_1\), \(\displaystyle BD\) felezőpontja pedig az \(\displaystyle F_2\) pont. Ezek koordinátái:

\(\displaystyle F_1\Big(\frac{a+c}{2}, 0\Big) \text { és } F_2\Big(0, \frac{b+d}{2}\Big).\)

Az \(\displaystyle F_1F_2\) egyenes egyenlete:

\(\displaystyle y=-\frac{\frac{b+d}{2}}{\frac{a+c}{2}}\cdot x+\frac{b+d}{2},\)

\(\displaystyle \text { azaz } y =-\frac{b+d}{a+c}\cdot x+\frac{b+d}{2}.\)

Behelyettesítéssel ellenőrizhető, hogy \(\displaystyle K\) valóban az egyenes pontja.

Ezzel még csak azt láttuk be, hogy azon az egyenesen rajta van. Most belátjuk, hogy a szakaszon is rajta van, vagyis, hogy az \(\displaystyle x\) koordinátája 0 és \(\displaystyle \frac{a+c}{2}\) közé esik (függetlenül \(\displaystyle \frac{a+c}{2}\) előjelétől). A \(\displaystyle K\) pont első koordinátája

\(\displaystyle \frac{bd(a+c)}{2(bd+ac)}=\frac{a+c}{2}\cdot \frac{bd}{bd+ac}.\)

Elég tehát azt belátni, hogy: \(\displaystyle 0<\frac{bd}{bd+ac}<1\). Mivel \(\displaystyle a\) és \(\displaystyle b\) pozitív, \(\displaystyle c\) és \(\displaystyle d\) pedig negatív, ezért a számláló és a nevező is negatív, így a kifejezés pozitív, vagyis nagyobb 0-nál. \(\displaystyle bd\) és \(\displaystyle ac\) is negatív, így \(\displaystyle \frac{bd}{bd+ac}<1\). Tehát \(\displaystyle K\) rajta van az \(\displaystyle F_1F_2\) szakaszon, és ezt szerettük volna belátni.

Molnár-Sáska Zoltán (Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium, Budapest, 9. évf.) dolgozata alapján.

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Andó Angelika, Cseh Kristóf, Csépai András, Döbröntei Dávid Bence, Fekete Panna, Kovács 972 Márton, Molnár-Sáska Zoltán, Nagy-György Pál, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Varga-Umbrich Eszter, Williams Kada.
4 pontot kapott:	Bereczki Zoltán, Dömsödi Bálint, Gáspár Attila, Kocsis Júlia, Lajkó Kálmán, Mócsy Miklós, Nagy Kartal, Nagy-György Zoltán, Sal Kristóf, Stein Ármin, Török Zsombor Áron, Wiandt Péter.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2015. januári matematika feladatai