A B. 4695. feladat (2015. február)

B. 4695. A sík pontjainak egy permutációjáról tudjuk, hogy ha három pont egy körön van, akkor a képeik is egy körön vannak. Mutassuk meg, hogy ennél a permutációnál három pont pontosan akkor van egy egyenesen, ha a képeik is egy egyenesen vannak.

(5 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

Megoldási ötlet: Mi lehet egy egyenes ősképe?

Megoldás. Először azt fogjuk belátni, hogy ha három pont képe egy egyenesre illeszkedik, akkor az eredeti pontok is egy egyenesre esnek.

Indirekt módon bizonyítunk. Tegyük fel, az állítással ellentétben, hogy létezik három olyan pont, amelyeknek a képe egy egyenesre esik, de az eredeti pontok nem illeszkednek egy egyenesre. Ekkor az eredeti három pont nem illeszkedik egy egyenesre, vagyis egy körre illeszkednek, tehát a feladatban adott feltétel alapján a képeik is. Itt viszont azonnal ellentmondásra jutunk, hiszen három pont nem illeszkedhet egyszerre egy körre és egy egyenesre is. A kiinduló feltételünk hamis, tehát ha három pont képe egy egyenesre esik, akkor az eredeti három pont is egy egyenesre esik.

A következőkben pedig azt fogjuk belátni, hogy ha három pont egy egyenesre esik, akkor a képeik is.

Most is gondolkodjunk indirekt módon. Tegyük fel, hogy létezik három olyan pont (\(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\)), amelyek egy egyenesre illeszkednek, de a képeik (\(\displaystyle A'\), \(\displaystyle B'\) és \(\displaystyle C'\)) nem. Ekkor az előbb belátott állítás értelmében az \(\displaystyle A'B'\), \(\displaystyle A'C'\) és \(\displaystyle B'C'\) egyeneseken elhelyezkedő pontok ősei azon az egyenesen vannak, amelyen \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\). Hiszen például tekintsünk egy \(\displaystyle D'\) pontot az \(\displaystyle A'B'\) egyenesen. Ekkor \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle D\) képei egy egyenesre illeszkednek, vagyis az első részben bizonyítottak szerint \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle D\) is egy egyenesre illeszkedik.

Most tekintsünk egy olyan \(\displaystyle E\) pontot, amely nem illeszkedik az \(\displaystyle AB\) egyenesre, és keressük meg a képét.

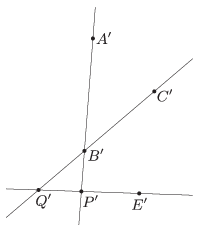
Vegyünk fel az \(\displaystyle A'B'\) egyenesen egy \(\displaystyle A'\)-től és \(\displaystyle B'\)-től különböző \(\displaystyle P'\) pontot, majd tekintsük az \(\displaystyle E'P'\) egyenest. Ez az egyenes az \(\displaystyle A'C'\) és \(\displaystyle B'C'\) egyenesek közül legalább az egyiket metszi, mivel legfeljebb csak az egyikkel lehet párhuzamos. Legyen az egyik ilyen metszéspont \(\displaystyle Q'\). Ekkor \(\displaystyle Q\), \(\displaystyle P\) és \(\displaystyle E\) pontok képei egy egyenesre illeszkednek, vagyis a \(\displaystyle Q\), \(\displaystyle P\) és \(\displaystyle E\) pontok is egy egyenesre esnek. Mivel \(\displaystyle Q'\) rajta van az \(\displaystyle A'C'\) vagy a \(\displaystyle B'C'\) egyenesen, \(\displaystyle P'\) pedig az \(\displaystyle A'B'\) egyenesen, így őseik, \(\displaystyle Q\) és \(\displaystyle P\) az \(\displaystyle AB\) egyenesen vannak. Ezért \(\displaystyle E\)-nek is az \(\displaystyle AB\) egyenesen kell lennie. Ez viszont ellentmondás, hiszen \(\displaystyle E\)-t úgy választottuk meg, hogy ne illeszkedjen az \(\displaystyle AB\) egyenesre. Vagyis a kiinduló feltétel hamis, azaz ha három pont egy egyenesre esik, akkor a képeik is egy egyenesre esnek.

Ezzel beláttuk azt az állítást, hogy három pont akkor és csak akkor van egy egyenesen, ha a képeik is egy egyenesen vannak.

Tóth Viktor (Kaposvári Táncsics Mihály Gimn., 10. évf.) dolgozata alapján

Statisztika:

41 dolgozat érkezett.
5 pontot kapott:	Baran Zsuzsanna, Cseh Kristóf, Csépai András, Czirkos Angéla, Döbröntei Dávid Bence, Fekete Panna, Gáspár Attila, Imolay András, Kerekes Anna, Kocsis Júlia, Kőrösi Ákos, Lajkó Kálmán, Molnár-Sáska Zoltán, Nagy Kartal, Nagy-György Pál, Németh 123 Balázs, Porupsánszki István, Schrettner Bálint, Szebellédi Márton, Szőke Tamás, Tóth Viktor, Varga-Umbrich Eszter, Williams Kada, Záhorský Ákos, Zolomy Kristóf.
4 pontot kapott:	Keresztfalvi Bálint.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	8 versenyző.

A KöMaL 2015. februári matematika feladatai