A B. 4702. feladat (2015. március)

B. 4702. Mutassuk meg, hogy végtelen sok olyan pont létezik, amely egy adott kocka három páronként kitérő élegyenesétől egyenlő távolságra van.

(5 pont)

A beküldési határidő 2015. április 10-én LEJÁRT.

Megoldási ötlet: Keressünk szimmetriatengelyt.

Megoldás. Egy kocka bármely éle a kockának két lapján van rajta és két csúcsát tartalmazza. Mivel kitérő egyenesek nincsenek egy síkban, ezért a kocka minden lapsíkján a három páronként kitérő élegyenes közül pontosan egy van rajta és a kocka nyolc csúcsa közül pontosan kettő olyan van, amelyiken a három páronként kitérő élegyenes közül egyik sem megy át.

Feltehető, hogy az \(\displaystyle ABCDEFGH\) kocka három páronként kitérő élegyenese közül az egyik a \(\displaystyle BC\) (1. ábra). Ekkor a kocka \(\displaystyle A\)-n, illetve \(\displaystyle D\)-n átmenő élegyenesei közül csak az egymással párhuzamos \(\displaystyle AE\) és \(\displaystyle DH\) egyenesek kitérők \(\displaystyle BC\)-vel. Ezért a három páronként kitérő élegyenes az \(\displaystyle ABCD\) lapnak legfeljebb három csúcsát tartalmazza. Ez nyilván a kocka bármely lapjára igaz, ezért minden lapon van legalább egy olyan csúcs, melyet a három páronként kitérő élegyenes egyike sem tartalmaz. De mivel az ilyen csúcsok száma kettő, és minden csúcsra a kockának három lapja illeszkedik, ezért ez azt jelenti, hogy a három páronként kitérő élegyenes által nem tartalmazott két csúcsra a kocka hat lapja közül három-háromnak kell illeszkednie, tehát a két nem tartalmazott csúcs a kocka egy testátlójának két végpontja kell, hogy legyen.

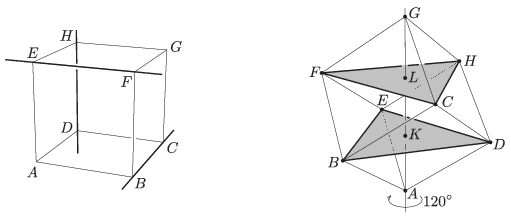
1. ábra                                                                       2. ábra

A kockának a \(\displaystyle BC\) él felezőmerőleges síkjára való szimmetriája miatt feltehetjük, hogy ez a testátló \(\displaystyle AG\). Ekkor a \(\displaystyle D\)-n átmenő élek közül \(\displaystyle DH\) kell, hogy szerepeljen a három páronként kitérő élegyenes közt, s ezért a harmadik egyenes csak \(\displaystyle EF\) lehet.

Megmutatjuk, hogy az \(\displaystyle AG\) testátló minden pontja egyenlő távolságra van a \(\displaystyle BC\), \(\displaystyle DH\) és \(\displaystyle EF\) egyenesektől. Ehhez elegendő belátnunk, hogy a testátló körüli \(\displaystyle 120^{\circ}\)-os forgatások a három egyenest ciklikusan permutálják, mert ebből a forgatás szögtartása miatt következik, hogy a testátló egy tetszőleges \(\displaystyle T\) pontjából a \(\displaystyle BC\), \(\displaystyle DH\) és \(\displaystyle EF\) egyenesekre bocsájtott merőlegeseket is permutálják a forgatások, azaz \(\displaystyle T\) egyenlő távolságra van a három egyenestől.

A \(\displaystyle BDE\) és \(\displaystyle CFH\) háromszögek szabályosak, mert mindegyik oldaluk hossza megegyezik a kocka lapátlójának hosszával. Legyen \(\displaystyle K\), illetve \(\displaystyle L\) e két szabályos háromszög középpontja. Mivel \(\displaystyle AB=AD=AE\) és \(\displaystyle GB=GD=GE\), ezért \(\displaystyle A\) is és \(\displaystyle G\) is rajta van a \(\displaystyle BDE\) háromszög síkjára \(\displaystyle K\)-ban állított merőlegesen, azaz \(\displaystyle AG\) merőleges a \(\displaystyle BDE\) háromszög síkjára és átmegy \(\displaystyle K\)-n. Az \(\displaystyle AC=AF=AH\) és \(\displaystyle GC=GF=GH\) egyenlőségekből pedig ugyanígy az következik, hogy \(\displaystyle AG\) merőleges a \(\displaystyle CFH\) háromszög síkjára is és átmegy \(\displaystyle L\)-en is. Ezért az \(\displaystyle AG\) körüli \(\displaystyle 120^{\circ}\)-os forgatásnál \(\displaystyle B\), \(\displaystyle D\) és \(\displaystyle E\) egy \(\displaystyle K\) középpontú körön mozog és \(\displaystyle B\mapsto D\), \(\displaystyle D\mapsto E\) és \(\displaystyle E\mapsto B\), míg \(\displaystyle C\), \(\displaystyle H\) és \(\displaystyle F\) egy \(\displaystyle L\) középpontú körön mozog és \(\displaystyle C\mapsto H\), \(\displaystyle H \mapsto F\) és \(\displaystyle F\mapsto C\) (2. ábra). Ez pedig azt jelenti, hogy a három kitérő egyenesre \(\displaystyle BC\mapsto DH\), \(\displaystyle DH \mapsto EF\) és \(\displaystyle EF\mapsto BC\), amit bizonyítani akartunk.

Statisztika:

64 dolgozat érkezett.
5 pontot kapott:	Andó Angelika, Baran Zsuzsanna, Bursics Balázs, Cseh Kristóf, Csépai András, Czirkos Angéla, Döbröntei Dávid Bence, Fekete Panna, Gál Boglárka, Gál Hanna, Gáspár Attila, Gyulai-Nagy Szuzina, Hansel Soma, Imolay András, Katona Dániel, Kerekes Anna, Keresztfalvi Bálint, Kocsis Júlia, Kosztolányi Kata, Kovács 526 Tamás, Kovács Balázs Marcell, Lajkó Kálmán, Lakatos Ádám, Nagy Dávid Paszkál, Nagy Kartal, Nagy-György Pál, Nagy-György Zoltán, Németh 123 Balázs, Nguyen Viet Hung, Olexó Gergely, Polgár Márton, Porupsánszki István, Regős Krisztina, Schrettner Bálint, Schwarcz Tamás, Szakács Lili Kata, Szebellédi Márton, Széles Katalin, Telek Máté László, Tóth Viktor, Váli Benedek, Varga-Umbrich Eszter, Várkonyi Dorka, Wiandt Péter, Williams Kada.
4 pontot kapott:	10 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2015. márciusi matematika feladatai