A B. 4710. feladat (2015. április)

B. 4710. A síkbeli \(\displaystyle \mathcal P\) ponthalmazról tudjuk, hogy minden egységsugarú körlemez a belsejében tartalmazza legalább egy pontját. Igaz-e, hogy biztosan van olyan egységsugarú zárt körlemez, amely legalább három \(\displaystyle \mathcal P\)-beli pontot tartalmaz?

(4 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldási ötlet: Rajzoljunk a \(\displaystyle \mathcal P\) -beli pontok körül egységsugarú köröket.

Megoldás. Megmutatjuk, hogy van olyan egységsugarú zárt körlemez, amely legalább három \(\displaystyle \mathcal{P}\)-beli pontot tartalmaz. A megoldás során tetszőleges \(\displaystyle A\) pont esetén \(\displaystyle k_A\) az \(\displaystyle A\) középpontú egységsugarú zárt körlemezt jelöli.

Először azt látjuk be, hogy van két olyan \(\displaystyle \mathcal{P}\)-beli pont, melyek távolsága kisebb, mint \(\displaystyle 2\). Legyen \(\displaystyle P_1\in \mathcal{P}\) tetszőleges halmazbeli pont, \(\displaystyle Q\) pedig olyan pont, melyre \(\displaystyle P_1Q=1\). Ekkor \(\displaystyle k_Q\) nem tartalmazza a belsejében \(\displaystyle P_1\)-et, ezért a feltételek szerint van olyan \(\displaystyle P_2\in \mathcal{P}\) pont, melyet \(\displaystyle k_Q\) a belsejében tartalmaz. Ekkor \(\displaystyle P_1P_2\) rövidebb, mint \(\displaystyle k_Q\) átmérője, azaz \(\displaystyle P_1P_2<2\) (1. ábra).

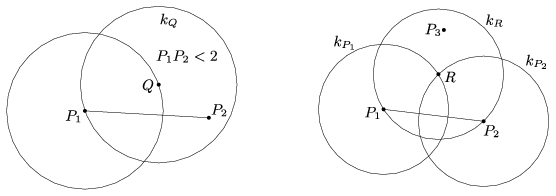
1. ábra                                                        2. ábra

Ezért van olyan \(\displaystyle R\) pont (a \(\displaystyle P_1\), illetve \(\displaystyle P_2\) középpontú 1 sugarú körvonalak két metszéspontja közül az egyik), melyre \(\displaystyle RP_1=RP_2=1\). Tehát \(\displaystyle k_R\) nem tartalmazza a belsejében sem \(\displaystyle P_1\)-et, sem \(\displaystyle P_2\)-t, ezért a feltételek szerint van olyan \(\displaystyle P_3\in \mathcal{P}\) pont, melyet \(\displaystyle k_R\) a belsejében tartalmaz (2. ábra). Vagyis \(\displaystyle k_R\) tartalmazza a \(\displaystyle P_1\), \(\displaystyle P_2\) és \(\displaystyle P_3\) pontok mindegyikét, s ezzel állításunkat beláttuk.

Czirkos Angéla (Kecskemét, Bolyai J. Gimn., 10. évf.) dolgozata alapján

Statisztika:

45 dolgozat érkezett.
4 pontot kapott:	Alexy Marcell, Baran Zsuzsanna, Bereczki Zoltán, Bursics Balázs, Csépai András, Czirkos Angéla, Döbröntei Dávid Bence, Fekete Panna, Gál Boglárka, Glasznova Maja, Gyulai-Nagy Szuzina, Hansel Soma, Imolay András, Katona Dániel, Kerekes Anna, Keresztfalvi Bálint, Kocsis Júlia, Kőrösi Ákos, Kuchár Zsolt, Lajkó Kálmán, Leitereg Miklós, Molnár-Sáska Zoltán, Nagy Kartal, Nagy-György Pál, Nagy-György Zoltán, Németh 123 Balázs, Polgár Márton, Porupsánszki István, Sal Kristóf, Schrettner Bálint, Schwarcz Tamás, Siemelink Johanna, Somogyi Pál, Szakács Lili Kata, Szakály Marcell, Szebellédi Márton, Tóth Viktor, Vágó Ákos, Váli Benedek, Várkonyi Dorka, Wiandt Péter, Williams Kada, Zolomy Kristóf.
3 pontot kapott:	Simon Dániel Gábor.
0 pontot kapott:	1 versenyző.

A KöMaL 2015. áprilisi matematika feladatai