A B. 4741. feladat (2015. november)

B. 4741. Hány olyan tengelyesen szimmetrikus háromszög van, melynek egyik oldala kétszer olyan hosszú, mint a háromszög valamelyik magassága, ha az egymáshoz hasonló háromszögeket nem tekintjük különbözőnek?

(3 pont)

A beküldési határidő 2015. december 10-én LEJÁRT.

Megoldásvázlat. Négy eset lehetséges:

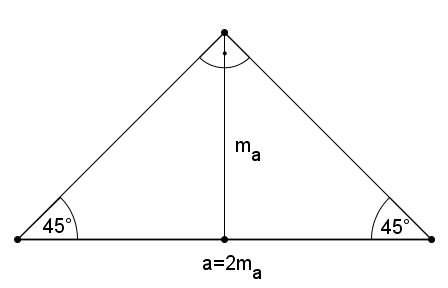
1. Az egyenlő szárú háromszögnek az alapja kétszer olyan hosszú, mint az alaphoz tartozó magasság. Ekkor a hasonlóságtól eltekintve egy megoldás van. A háromszög szögei \(\displaystyle 90^{\circ}\), \(\displaystyle 45^{\circ}\), \(\displaystyle 45^{\circ}\).

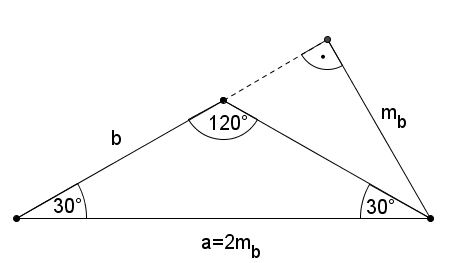
2. Az egyenlő szárú háromszögnek az alapja kétszer olyan hosszú, mint a szárakhoz tartozó magasság. A hasonlóságtól eltekintve ekkor is csak egy megoldás van. A háromszög szögei \(\displaystyle 120^{\circ}\), \(\displaystyle 30^{\circ}\), \(\displaystyle 30^{\circ}\).

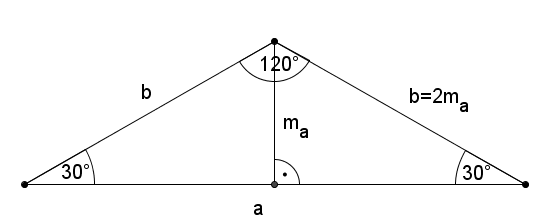
3. A háromszög szárai kétszer olyan hosszúak, mint az alaphoz tartozó magasság. Ekkor egy eset van. A háromszög szögei \(\displaystyle 120^{\circ}\), \(\displaystyle 30^{\circ}\), \(\displaystyle 30^{\circ}\). Ez viszont megegyezik az előző eset megoldásával.

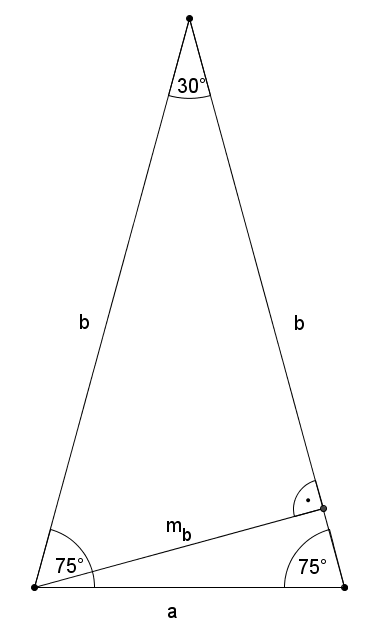
4. A háromszög szárai kétszer olyan hosszúak, mint a szárakhoz tartozó magasság. Ekkor két eset van. Ha a háromszög hegyesszögű, akkor szögei \(\displaystyle 30^{\circ}\), \(\displaystyle 75^{\circ}\), \(\displaystyle 75^{\circ}\).

Ha a háromszög tompaszögű, akkor szögei \(\displaystyle 150^{\circ}\), \(\displaystyle 15^{\circ}\), \(\displaystyle 15^{\circ}\).

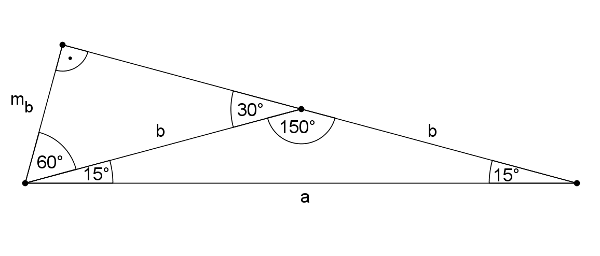
Tehát négy olyan háromszöget találtunk, ami megfelel a feladat feltételeinek.

Statisztika:

192 dolgozat érkezett.
3 pontot kapott:	Andó Angelika, Bindics Boldizsár, Busa 423 Máté, Csertán András, Csiszár Zoltán, Csorba Benjámin, Erdődi Ádám Károly, Ferenczi László, Geretovszky Anna, György Levente, Horváth András János, Hunyadi Marcell, Jakus Balázs István, Janzer Orsolya Lili, Kardos Bálint Tamás, Kocsis Júlia, Kosztolányi Kata, Kővári Péter Viktor, Mikulás Zsófia, Mona Zsuzsa, Noszály Áron, Póka Lili , Polgár Márton, Pusztai Bertalan, Schrettner Bálint, Schrettner Jakab, Somogyi Pál, Szabó 417 Dávid, Szajbély Sámuel, Szajbély Zsigmond, Szakály Marcell, Török Zsombor Áron, Tubak Dániel, Ujvári Bors Benedek, Vágó Richárd, Vári-Kakas Andor, Várkonyi Dorka, Varsányi András, Weisz Máté, Xu Dávid.
2 pontot kapott:	116 versenyző.
1 pontot kapott:	17 versenyző.
0 pontot kapott:	15 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2015. novemberi matematika feladatai