A B. 4743. feladat (2015. november)

B. 4743. Az \(\displaystyle ABC\) háromszög beírható köre a \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) oldalakat rendre az \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) pontban érinti. Legyenek az \(\displaystyle AC_1B_1\), \(\displaystyle BA_1C_1\) és \(\displaystyle CB_1A_1\) háromszögek magasságpontjai rendre \(\displaystyle M_A\), \(\displaystyle M_B\) és \(\displaystyle M_C\). Mutassuk meg, hogy az \(\displaystyle A_1B_1C_1\) háromszög egybevágó az \(\displaystyle M_AM_BM_C\) háromszöggel.

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

A beküldési határidő 2015. december 10-én LEJÁRT.

Megoldásvázlat.

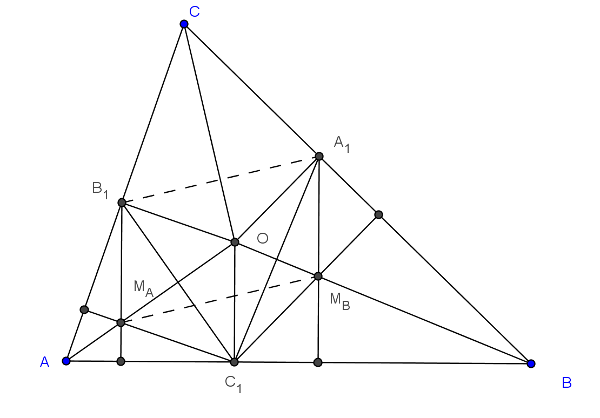
Legyen a beírt kör középpontja az \(\displaystyle O\) pont. Külső pontból egy körhöz húzott érintőszakaszok egyenlő hosszúságúak, tehát az \(\displaystyle AB_1C_1\) háromszög egyenlő szárú, emiatt az \(\displaystyle AB_1C_1\) háromszög \(\displaystyle M_{A}\) magasságpontja rajta van az \(\displaystyle A\)-hoz tartozó belső szögfelezőn. \(\displaystyle OC_{1}\) párhuzamos \(\displaystyle B_1M_{A}\)-val, mivel mindkettő merőleges \(\displaystyle AB\)-re, továbbá \(\displaystyle OB_1\) párhuzamos \(\displaystyle C_{1}M_{A}\)-val, mivel merőlegesek \(\displaystyle AC\)-re. Ezek alapján \(\displaystyle M_{A}C_{1}OB_{1}\) szemközti oldalai párhuzamosak, tehát parallelogramma. Látjuk azt is, hogy \(\displaystyle M_{A}B_1 = OC_1\), a beírt kör \(\displaystyle r\) sugarával egyenlőek. Hasonlóan \(\displaystyle A_1M_{B}C_{1}O\) is parallelogramma. Emiatt \(\displaystyle A_1M_{B} = OC_{1} = r\). Az eddigiek alapján \(\displaystyle M_{A}B_{1} = A_1M_{B} = r\), és párhuzamosak is, hiszen merőlegesek \(\displaystyle AB\)-re, vagyis \(\displaystyle M_{A}B_1A_1M_{B}\) parallelogramma. Ebből már látható, hogy \(\displaystyle A_1B_1 = M_{A}M_{B}\).

Hasonlóan igazolható, hogy \(\displaystyle A_1C_1 = M_{A}M_{C}\) és \(\displaystyle B_1C_1 = M_{B}M_{C}\).

Tehát az \(\displaystyle A_1B_1C_1\) háromszög egybevágó az \(\displaystyle M_{A}M_{B}M_{C}\) háromszöggel.

Statisztika:

111 dolgozat érkezett.
4 pontot kapott:	88 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	3 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2015. novemberi matematika feladatai