 |
A B. 4746. feladat (2015. november) |
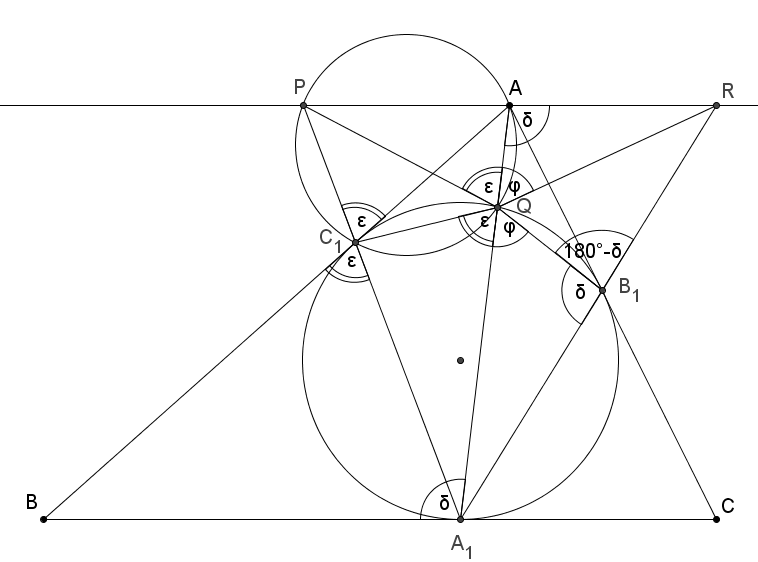
B. 4746. Az \(\displaystyle ABC\) háromszög beírható köre a \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) oldalakat rendre az \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) pontban érinti. Az \(\displaystyle AA_1\) szakasznak a beírható körrel való másik metszéspontja \(\displaystyle Q\). Az \(\displaystyle A\) ponton átmenő, \(\displaystyle BC\)-vel párhuzamos egyenest az \(\displaystyle A_1 C_1\) és \(\displaystyle A_1 B_1\) egyenesek a \(\displaystyle P\) és \(\displaystyle R\) pontban metszik. Igazoljuk, hogy \(\displaystyle PQR\sphericalangle =B_1 QC_1\sphericalangle\).
(Kvant)
(5 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldásvázlat. Legyen az \(\displaystyle A_1B_1Q\angle=\delta\). Ez a szög a háromszögbe írt körben az \(\displaystyle A_1C_1Q\) íven nyugvó kerületi szög. Ugyanehhez az ívhez tartozó érintő szárú kerületi szög a \(\displaystyle QA_1B\angle\). Így ez a két szög egyenlő.
\(\displaystyle A_1AR\angle=QA_1B\angle=\delta\), mert váltószögek, hiszen \(\displaystyle PR\parallel BC\).
Az \(\displaystyle AQB_1R\) négyszögben a \(\displaystyle B_1\) csúcsnál lévő szög \(\displaystyle 180^{\circ}-\delta\), az \(\displaystyle A\) csúcsnál lévő szög \(\displaystyle \delta\), vagyis a négyszög szemben lévő szögeinek összege \(\displaystyle 180^{\circ}\), tehát húrnégyszög. Hasonlóan belátható, hogy az \(\displaystyle AQC_1P\) négyszög is húrnégyszög.
Legyen az \(\displaystyle A_1QC_1\angle=\varepsilon\). Ez a szög a háromszögbe írt körben az \(\displaystyle A_1C_1\) íven nyugvó kerületi szög. Ugyanehhez az ívhez tartozó érintő szárú kerületi szög az \(\displaystyle A_1C_1B\angle\). Így ez a két szög egyenlő. \(\displaystyle A_1C_1B\angle=PC_1A\angle=\varepsilon\), mert csúcsszögek.
Az \(\displaystyle AQC_1P\) húrnégyszögben \(\displaystyle PC_1A\angle=PQA\angle=\varepsilon\), mert azonos íven nyugvó kerületi szögek. Így beláttuk, hogy \(\displaystyle A_1QC_1\angle=PQA\angle=\varepsilon\).
Hasonlóan beláthatjuk, hogy \(\displaystyle A_1QB_1\angle=AQR\angle=\varphi\).
Tehát \(\displaystyle PQR\angle=\varepsilon+\varphi=B_1QC_1\angle\), és ezt kellett igazolnunk.
Statisztika:
77 dolgozat érkezett. 5 pontot kapott: 62 versenyző. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2015. novemberi matematika feladatai
