 |
A B. 4748. feladat (2015. november) |
B. 4748. Forgassuk meg a \(\displaystyle \mathcal H\) háromszöget egy, a síkjában fekvő, de őt nem metsző egyenes körül. Bizonyítsuk be, hogy a keletkezett test térfogata megegyezik \(\displaystyle \mathcal H\) területének és a \(\displaystyle \mathcal H\) súlypontja által a forgatás során leírt kör kerületének a szorzatával.
(Figyelem! A feladat a lapban pontatlanul jelent meg.)
(5 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldás.
Legyenek a háromszög csúcsainak távolságai a \(\displaystyle t_1\) forgástengelytől \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) az ábra szerint.
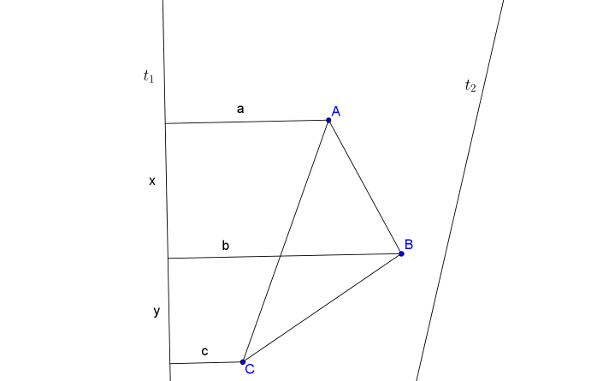
A keletkezett test térfogatát - az ábrán szereplő elhelyezkedés és adatok alapján - úgy is kiszámíthatjuk, hogy vesszük az \(\displaystyle a\) és \(\displaystyle b\) sugarú és \(\displaystyle x\) magasságú csonkakúp, továbbá a \(\displaystyle b\) és \(\displaystyle c\) sugarú és \(\displaystyle y\) magasságú csonkakúpok térfogatának összegét, majd ebből kivonjuk az \(\displaystyle a\) és \(\displaystyle c\) sugaú \(\displaystyle (x+y)\) magasságú csonkakúp térfogatát.
A csonkakúp térfogatképletét felhasználva így:
\(\displaystyle \frac{x\cdot\pi\cdot(a^2+ab+b^2)+y\cdot\pi\cdot(b^2+bc+c^2)-(x+y)\cdot\pi\cdot(a^2+ac+c^2)}{3}.\)
Erről kell belátnunk, hogy egyenlő a súlypont által leírt kör kerületének és a háromszög területének szorzatával. A súlypont által leírt kör kerülete
\(\displaystyle \frac{2\cdot \pi \cdot (a+b+c)}{3}.\)
A háromszög területe az ábrán szereplő adatokkal meghatározható úgy, hogy az \(\displaystyle a\), \(\displaystyle b\) alapú \(\displaystyle x\) magasságú trapéz, továbbá a \(\displaystyle b\), \(\displaystyle c\) alapú \(\displaystyle y\) magasságú trapéz területének összegéből levonjuk az \(\displaystyle a\), \(\displaystyle c\) alapú \(\displaystyle x+y\) magasságú trapéz területét:
\(\displaystyle \frac{(a+b)\cdot x}{2}+\frac{(b+c)\cdot y}{2}-\frac{(a+c)\cdot(x+y)}{2}=\frac{ax+bx+by+cy-ax-cx-ay-cy}{2}=\)
\(\displaystyle =\frac{bx-cx+by-ay}{2}.\)
A kerület és a terület szorzata egyszerűsítés után:
\(\displaystyle \frac{\pi\cdot(a+b+c)(bx-cx+by-ay)}{3}.\)
Alakítsuk most azonosan a csonkakúpokból nyert térfogatképletet:
\(\displaystyle \frac{\pi}{3} \Big[ x(a^{2}+ab+b^{2})-x(a^{2}+ac+c^{2})+y(b^{2}+bc+c^{2})-y(a^{2}+ac+c^{2})\Big]=\)
\(\displaystyle =\frac{\pi}{3} \Big[x(ab-ac+b^{2}-c^{2})+y(b^{2}-a^{2}+bc-ac)\Big]=\)
\(\displaystyle =\frac{\pi}{3} \Big[x\big(a(b-c)+(b+c)(b-c)\big)+y\big((b-a)(b+a)+c(b-a)\big)\Big]=\)
\(\displaystyle =\frac{\pi}{3} \Big[x(b-c)(a+b+c)+y(b-a)(a+b+c)\Big]=\)
\(\displaystyle =\frac{\pi}{3}(a+b+c)(bx-cx+by-ay).\)
A kétféleképpen számolt térfogat megegyezik, erre az esetre igazoltuk az állítást. Eltérő számolást kapunk, ha pl. a \(\displaystyle t_{2}\) tengelynek megfelelő tengely körül forgatjuk meg a háromszöget. A kétféle számolás egyezősége azonban ebben az esetben is ugyanezekkel a lépésekkel végezhető el.
Statisztika:
68 dolgozat érkezett. 5 pontot kapott: Andó Angelika, Barabás Ábel, Baran Zsuzsanna, Borbényi Márton, Bukva Balázs, Busa 423 Máté, Csahók Tímea, Cseh Kristóf, Csorba Benjámin, Czirkos Angéla, Döbröntei Dávid Bence, Fekete Balázs Attila, Fülöp Anna Tácia, Gáspár Attila, Hansel Soma, Harsányi Benedek, Horváth András János, Imolay András, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kocsis-Savanya Miklós, Kovács 162 Viktória, Kovács 246 Benedek, Lajkó Kálmán, Lakatos Ádám, Matolcsi Dávid, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Nagy Nándor, Németh 123 Balázs, Nguyen Viet Hung, Pálfy Máté András, Paulovics Péter, Polgár Márton, Radnai Bálint, Sal Kristóf, Schrettner Bálint, Souly Alexandra, Szécsényi Nándor, Tóth 2 Rudolf, Tóth Viktor, Vághy Mihály, Váli Benedek, Varjas István Péter, Várkonyi Dorka. 4 pontot kapott: 13 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2015. novemberi matematika feladatai
