 |
A B. 4749. feladat (2015. november) |
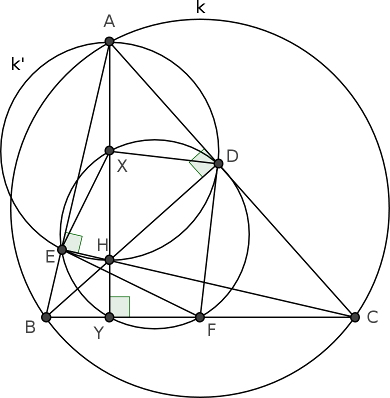
B. 4749. A hegyesszögű \(\displaystyle ABC\) háromszög \(\displaystyle B\) és \(\displaystyle C\) csúcsából induló magasságvonal talppontja az \(\displaystyle AC\), illetve \(\displaystyle AB\) oldalon rendre \(\displaystyle D\) és \(\displaystyle E\), a \(\displaystyle BC\) oldal felezőpontja \(\displaystyle F\). Az \(\displaystyle AF\) és \(\displaystyle DE\) szakaszok metszéspontja \(\displaystyle M\), az \(\displaystyle M\) pontnak a \(\displaystyle BC\) szakaszra eső merőleges vetülete \(\displaystyle N\). Bizonyítsuk be, hogy az \(\displaystyle AN\) szakasz felezi a \(\displaystyle DE\) szakaszt.
Tanára, dr. Kálmán Attila emlékére javasolta Bíró Bálint (Eger)
(6 pont)
A beküldési határidő 2015. december 10-én LEJÁRT.
Megoldás. Jelöljük \(\displaystyle k\)-val, illetve \(\displaystyle k'\)-vel az \(\displaystyle ABC\), illetve az \(\displaystyle ADE\) háromszög köré írt kört. Jól ismert, hogy az \(\displaystyle FE\) és \(\displaystyle FD\) szakaszok érintik \(\displaystyle k'\)-t. Ennek egy bizonyítása a következő: legyen az \(\displaystyle ABC\) háromszögben \(\displaystyle H\) a magyasságpont, az \(\displaystyle AH\) szakasz felezőpontja \(\displaystyle X\), az \(\displaystyle A\)-ból induló magasság talppontja \(\displaystyle Y\). A \(\displaystyle D\)-nél és \(\displaystyle E\)-nél levő derékszögek miatt \(\displaystyle H\) is a \(\displaystyle k'\) körön van, a \(\displaystyle k'\)-nek az \(\displaystyle AH\) szakasz átmérője, \(\displaystyle X\) a kör középpontja. A \(\displaystyle D,E,F,X,Y\) pontok egy körön, az \(\displaystyle ABC\) háromszög Feuerbach-körén vannak, ezért \(\displaystyle FEX\angle=FYX\angle=CYA\angle=90^\circ\), és hasonlóan \(\displaystyle FDX\angle=90^\circ\). Az \(\displaystyle FD\) és \(\displaystyle FE\) szakaszok merőlegesek a \(\displaystyle k'\) kör \(\displaystyle XD\), illetve \(\displaystyle XE\) sugaraira, tehát érintik \(\displaystyle k'\)-t. (A bizonyítás közvetlenül, a Feuerbach kör használata nélkül is lehetséges, például az \(\displaystyle EXA\) és \(\displaystyle EFC\) háromszögek hasonlóságából.)
Szintén jól ismert, hogy az \(\displaystyle ABC\) háromszög hasonló az \(\displaystyle ADE\) háromszöghöz. (Az \(\displaystyle A\) csúcsnál levő szögük közös; a \(\displaystyle D,E\) pontok a \(\displaystyle BC\) szakasz Thalész-körén vannak, így például \(\displaystyle CBA\angle=180^\circ-EDC\angle=ADE\angle\).) Legyen \(\displaystyle b\), illetve \(\displaystyle c\) a \(\displaystyle B\) és \(\displaystyle C\) pontokban \(\displaystyle k\)-hoz húzott érintő egyenes; metszéspontjukat jelöljük \(\displaystyle P\)-vel. Legyen továbbá \(\displaystyle d=FD\) és \(\displaystyle e=FE\) a \(\displaystyle k'\)-höz \(\displaystyle D\)-ben, illetve \(\displaystyle E\)-ben húzott érintő, \(\displaystyle G\) a \(\displaystyle DE\) szakasz felezőpontja és \(\displaystyle N_1=AP\cap BC\). (Később meg fogjuk mutatni, hogy \(\displaystyle N_1\) azonos a feladatban megadott \(\displaystyle N\) ponttal.) A \(\displaystyle P\)-ből \(\displaystyle k\)-hoz húzott \(\displaystyle PB\) és \(\displaystyle PC\) érintő szakaszok egyenlő hosszúak, tehát a \(\displaystyle BCP\) háromszög egyenlő szárú, és \(\displaystyle PF\) a \(\displaystyle BC\) szakasz merőleges felezője.
Tekintsük azt a \(\displaystyle \varphi\) hasonlósági transzformációt, ami az \(\displaystyle ABC\) háromszöget az \(\displaystyle ADE\) háromszögbe viszi. Ekkor tehát \(\displaystyle \varphi(A)=A\), \(\displaystyle \varphi(B)=D\) és \(\displaystyle \varphi(C)=E\). A hasonlóság körülírt kört körülírt körbe, érintőt érintőbe, felezőpontot felezőpontba, metszéspontot metszéspontba képez, ezért \(\displaystyle \varphi(k)=k'\), \(\displaystyle \varphi(b)=d\), \(\displaystyle \varphi(c)=e\), \(\displaystyle \varphi(F)=G\), \(\displaystyle \varphi(P)=\varphi(b\cap c)=d\cap e=F\) és \(\displaystyle \varphi(N_1)=\varphi(AP\cap BC)=AF\cap DE=M\).
A hasonlóság a \(\displaystyle CAF\angle\) és a \(\displaystyle BAP\angle\) szöget az \(\displaystyle EAG\angle\), illetve a \(\displaystyle DAF\angle\) szögbe viszi, ezért \(\displaystyle BAG\angle = EAG\angle = CAF \angle = DAF\angle = BAP\angle\). Tehát \(\displaystyle BAG\angle = BAP\angle\); ebből látjuk, hogy \(\displaystyle G\) az \(\displaystyle AP\) egyenesen van.
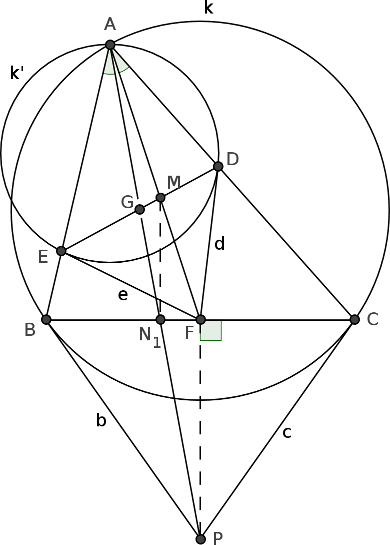
A hasonlóság az \(\displaystyle A,N_1,P\) pontokat rendre az \(\displaystyle A,M,F\) pontokba viszi, ezért \(\displaystyle \frac{AN_1}{AP}=\frac{AM}{AF}\). A párhuzamos szelők tételének megfordítása szerint ebből következik, hogy \(\displaystyle MN_1||FP\), és emiatt \(\displaystyle FP\)-hez hasonlóan \(\displaystyle MN_1\) is merőleges \(\displaystyle BC\)-re. Ez viszont azt jelenti, hogy \(\displaystyle N_1\) az \(\displaystyle M\)-ből \(\displaystyle BC\)-re bocsátott merőleges talppontja, vagyis \(\displaystyle N_1=N\). Tehát az \(\displaystyle AN\) egyenes átmegy \(\displaystyle G\)-n, a \(\displaystyle DE\) szakasz felezőpontján. Az \(\displaystyle N\) a \(\displaystyle BC\) oldalnak belső pontja, így a \(\displaystyle DE\) egyenesnek \(\displaystyle A\)-val ellentétes oldalán van, tehát a \(\displaystyle G\) metszéspont az \(\displaystyle AN\) szakasz belsejében van.
Megjegyzés. A feladat ábrájában több nevezetes geometriai elrendezést felfedezhetünk. A \(\displaystyle P\) pont a \(\displaystyle BC\) egyenesnek a \(\displaystyle k\) körre vonatkozó pólusa. Az \(\displaystyle AP\) egyenes az \(\displaystyle ABC\) háromszög \(\displaystyle AF\) súlyvonalának tükörképe az \(\displaystyle A\)-ből induló szögfelezőre; ez az egyenes az \(\displaystyle A\)-ból induló szimmedián.
Hasonlóan, a \(\displaystyle k'\) körben az \(\displaystyle F\) pont a \(\displaystyle DE\) egyenes pólusa, és az \(\displaystyle AF\) egyenes az \(\displaystyle ADE\) háromszög \(\displaystyle A\)-ból induló szimmediánja.
Statisztika:
36 dolgozat érkezett. 6 pontot kapott: Barabás Ábel, Baran Zsuzsanna, Bodolai Előd, Bukva Balázs, Cseh Kristóf, Csorba Benjámin, Czirkos Angéla, Gáspár Attila, Hansel Soma, Horváth András János, Imolay András, Kerekes Anna, Keresztfalvi Bálint, Kocsis Júlia, Kovács 162 Viktória, Lajkó Kálmán, Lakatos Ádám, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Németh 123 Balázs, Polgár Márton, Radnai Bálint, Schrettner Bálint, Stein Ármin, Vághy Mihály, Vankó Miléna, Varga-Umbrich Eszter. 5 pontot kapott: Andó Angelika, Döbröntei Dávid Bence, Matolcsi Dávid. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2015. novemberi matematika feladatai
