 |
A B. 4756. feladat (2015. december) |
B. 4756. Adott az egységkocka belsejében néhány gömb, melyek felszínének összege 2015. Mutassuk meg, hogy
\(\displaystyle a)\) van olyan egyenes, amely ezek közül legalább 500 gömböt metsz,
\(\displaystyle b)\) van olyan sík, amely ezek közül legalább 600 gömböt metsz.
Erdélyi Magyar Matematikaverseny
(6 pont)
A beküldési határidő 2016. január 11-én LEJÁRT.
Megoldásvázlat. Legyenek a gömbök \(\displaystyle G_1,G_2,\ldots,G_n\), sugaraik rendre \(\displaystyle r_1,r_2, \ldots,r_n\). Mindegyik \(\displaystyle G_i\) a kocka belsejében van, ezért
| \(\displaystyle r_1,r_2,\ldots,r_n\le \frac12. \) | (1) |
Mindegyik \(\displaystyle i\) indexre a \(\displaystyle G_i\) felszíne \(\displaystyle 4\pi \cdot r_i^2\). A felszínek összegére vonatkozó feltételt tehát a következő alakba írhatjuk:
| \(\displaystyle r_1^2 + r_2^2 + \ldots + r_n^2 = \frac{2015}{4\pi}. \) | (2) |
\(\displaystyle a)\) Legyen \(\displaystyle L\) a kocka egyik lapja, és mindegyik \(\displaystyle i\) indexre legyen \(\displaystyle K_i\) a \(\displaystyle G_i\) gömb merőleges vetülete az \(\displaystyle L\) lapra. A \(\displaystyle K_i\) egy \(\displaystyle r_i\) sugarú körlemez, ami az \(\displaystyle L\) lap belsejében van. A vetületek összege nagyobb, mint az \(\displaystyle L\) területének \(\displaystyle 500\)-szorosa:
\(\displaystyle \sum_{i=1}^n \mathrm{t}(K_i) = \pi \sum_{i=1}^n r_i^2 = \pi \cdot \frac{2015}{4\pi} > 500 = 500\cdot \mathrm{t}(L). \)
Ezért van olyan \(\displaystyle X\) pontja az \(\displaystyle L\) lapnak, ami több, mint \(\displaystyle 500\) \(\displaystyle K_i\)-nek belső pontja. Ekkor az \(\displaystyle X\)-ben \(\displaystyle L\)-re állított merőleges egyenes metszi az ezekhez tartozó \(\displaystyle G_i\) gömböket.
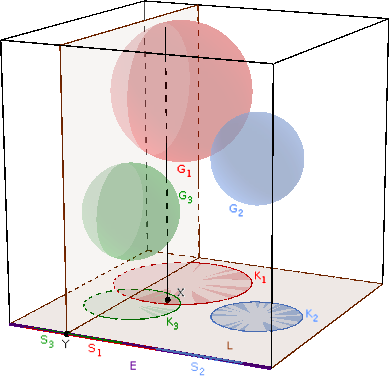
\(\displaystyle b)\) Legyen most \(\displaystyle E\) a kocka egyik éle, és vetítsük a gömböket merőlegesen az \(\displaystyle E\) szakaszra. A \(\displaystyle G_i\) vetülete egy \(\displaystyle S_i\) szakasz, ennek hossza \(\displaystyle |S_i|=2r_i\le1\). Ebből következik, hogy \(\displaystyle |S_i|\ge|S_i|^2=4r_i^2\).
A vetületek hosszúságainak összege nagyobb, mint \(\displaystyle E\) hosszának \(\displaystyle 600\)-szorosa:
\(\displaystyle \sum_{i=1}^n |S_i| \ge \sum_{i=1}^n 4r_i^2 = \frac{2015}{\pi} > 600 = 600\cdot |E|. \)
Emiatt biztosan van olyan \(\displaystyle Y\in E\) pont, ami több, mint \(\displaystyle 600\) \(\displaystyle S_i\)-nek belső pontja. Ekkor a \(\displaystyle Y\)-ban \(\displaystyle E\)-re állított merőleges sík metszi az ezekhez tartozó \(\displaystyle G_i\) gömböket.
Statisztika:
42 dolgozat érkezett. 6 pontot kapott: Andó Angelika, Baran Zsuzsanna, Bodolai Előd, Borbényi Márton, Bukva Balázs, Busa 423 Máté, Csertán András, Czirkos Angéla, Dobák Dávid, Döbröntei Dávid Bence, Gáspár Attila, Hansel Soma, Imolay András, Juhász 326 Dániel, Kasó Ferenc, Kerekes Anna, Keresztes László, Keresztfalvi Bálint, Klász Viktória, Kovács 246 Benedek, Kővári Péter Viktor, Matolcsi Dávid, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Németh 123 Balázs, Páli Petra, Schefler Barna, Somogyi Pál, Souly Alexandra, Sudár Ákos, Szabó 864 Blanka, Szabó 997 Balázs István, Tóth Viktor, Váli Benedek, Záhorský Ákos, Zsigri Bálint. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2015. decemberi matematika feladatai

