A B. 4758. feladat (2015. december)

B. 4758. Legalább hány különböző oldalegyenese van egy (nem feltétlenül konvex) \(\displaystyle 2015\)-szögnek?

Javasolta: Lenger Dániel (Budapest)

(6 pont)

A beküldési határidő 2016. január 11-én LEJÁRT.

Megoldás. \(\displaystyle k\) egyenesnek legfeljebb \(\displaystyle \binom k2\) metszéspontja van, így \(\displaystyle \binom k2\) legalább 2015 kell, hogy legyen. Mivel \(\displaystyle \binom{64}{2}=2016\), így legalább 64 oldalegyenes van.

De ennyi nem elég, hiszen ekkor egy oldalegyenesen legfeljebb 63 metszéspont lehet, amelyek legfeljebb 62 (szomszédos) szakaszt alkotnak. Ebből a 62 szakaszból legfeljebb 31 lehet a 2015-szög oldala, ugyanis semelyik két oldal nem ér össze. Tehát legfeljebb \(\displaystyle 64\cdot31=1984\) oldal van, ami kevesebb 2015-nél.

Tehát legalább 65 egyenesre van szükség. Megmutatjuk, hogyan lehet jól kiválasztani 65 egyenest úgy, hogy egy 2015-szöget kapjunk.

Először vegyünk egy szabályos 65-szöget és legyenek az oldalegyenesei a választott egyenesek. Ki fogjuk használni a szabályos sokszög szimmetriáit.

Színezzük ki a keletkező szakaszokat. Egy egyenesen 63 szakasz található, felváltva lesznek kékek és pirosak, pirossal kezdve. Így a két szélső is piros lesz.

A szimmetriák miatt bármelyik egyenest forgatás viszi bármelyik másik egyenesbe úgy, hogy a színezés változatlan marad. Az alábbi két ábrán 13 egyenesre adtunk meg megfelelő színezést.

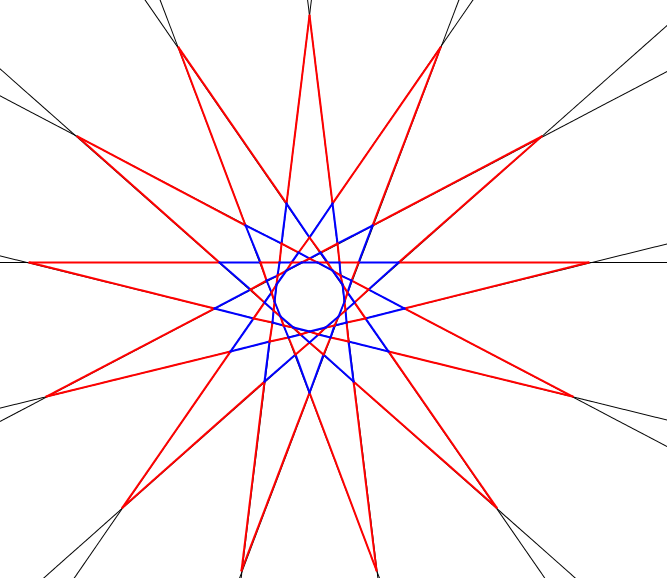
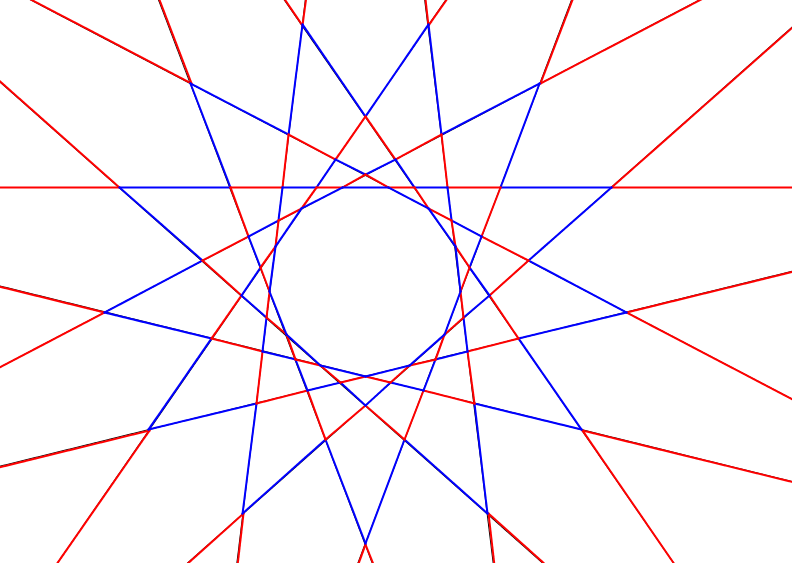
Az is teljesül, hogy a legkülső szakaszok egy piros 130-szöget alkotnak (amit ,,csillagnak'' fogunk nevezni), a velük szomszédos kék szakaszok szintén csillagot alkotnak, és így tovább. Mivel a 63 páratlan, ezért 16 piros és 15 kék csillag után, marad 65 kék szakasz, amik egy szabályos 65-szöget alkotnak. (Ez egyébként éppen az eredeti 65-szög, de ezt a tényt nem használjuk ki). Az ábrákon három piros csillag, két kék csillag és egy kék szabályos 13-szög látható.

Van \(\displaystyle 16\cdot130=2080\) piros szakasz, ezekből kiindulva készítjük el a 2015-szöget. A fenti, 13 egyenesből kiinduló ábrához hasonló ábra készíthető 65 egyenesre is. Válasszunk ki két szomszédos piros csillagot. A következő trükkel össze tudjuk őket kötni:

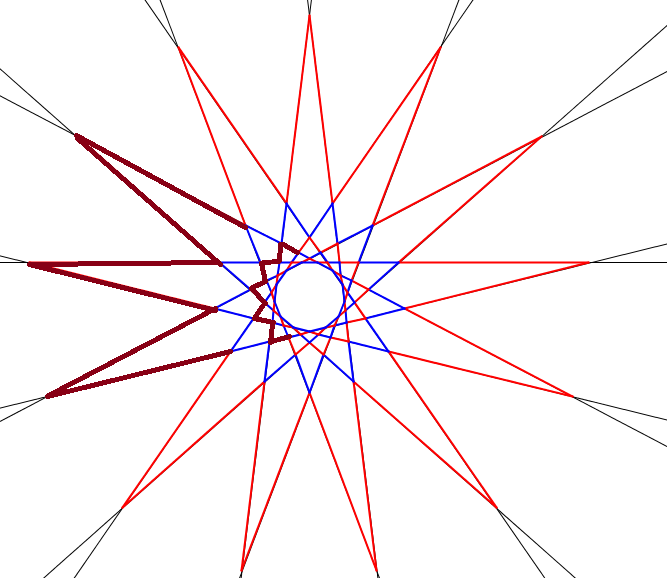
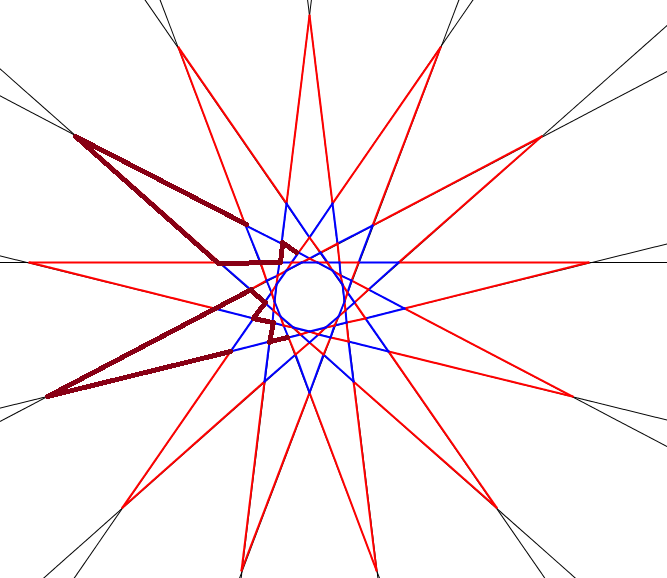
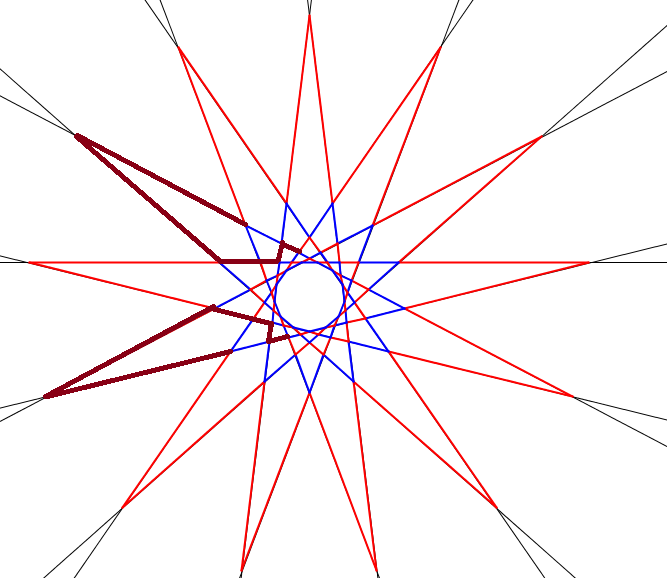
Néhány szakasz így bekerül a sokszögbe, néhány pedig kikerül belőle. Az első ábrán látható vékony piros szakaszok nem változnak, a sötétpirosak átmennek a második ábrán látható sötétpirosakba (néhány közülük nem változik). Ezzel a trükkel a piros oldalak száma 4-gyel csökkent.

Ezt a trükköt bármely két szomszédos piros csillagra alkalmazhatjuk.

Tehát az oldalak számát ily módon \(\displaystyle 15\cdot4=60\)-nal csökkentjük, és így egy 2020-szöget kapunk. Még 5-tel kell csökkenteni az oldalszámot.

Kicsit módosítjuk a trükkünket. Csinálunk néhány ,,le'' és ,,fel'' lépést:

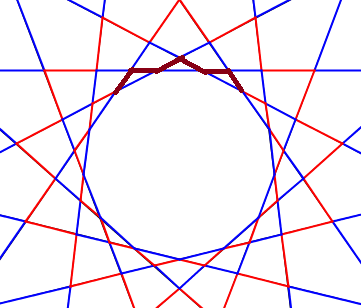
Így az oldalszám 6-tal csökken. Használjuk ezt egyszer az eredeti türkk helyett, így a kapott oldalszám 2018.

A maradék 3 oldalt középen nyerjük:

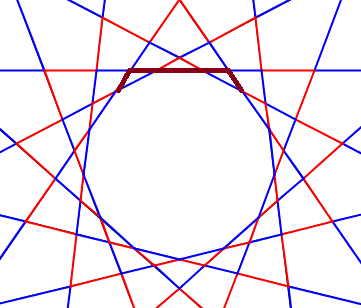
Statisztika:

29 dolgozat érkezett.
6 pontot kapott:	Baran Zsuzsanna, Borbényi Márton, Bukva Balázs, Gáspár Attila, Hansel Soma, Imolay András, Kovács 246 Benedek, Váli Benedek.
5 pontot kapott:	Lajkó Kálmán.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	8 versenyző.

A KöMaL 2015. decemberi matematika feladatai