 |
A B. 4767. feladat (2016. január) |
B. 4767. Határozzuk meg azokat a konvex poliédereket, amelyekre teljesül, hogy mindegyik \(\displaystyle C\) csúcs körül a csatlakozó lapok \(\displaystyle C\)-nél levő szögeinek összege pontosan \(\displaystyle 180^\circ\).
(6 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
Megoldás. Először bebizonyítjuk, hogy a poliéder tetraéder, utána pedig megmutatjuk, hogy csak ún. egyenlő oldalú tetraéder lehet (amelyben a szemközti élek egyforma hosszúak, és a lapok egybevágók).
Egyenlő oldalú tetraéderekre triviálisan teljesül, hogy a csúcsok körül a szögek összege \(\displaystyle 180^\circ\).
I. Jelölje \(\displaystyle L\), \(\displaystyle E\) és \(\displaystyle C\) a poliéder lapjainak, éleinek, illetve csúcsainak számát. Az Euler-féle poliédertétel szerint \(\displaystyle L+C = E+2\), átrendezve
| \(\displaystyle E = L+C-2. \) | (1) |
Az egyes lapok oldalszáma legyen \(\displaystyle d_1,d_2,\ldots,d_L\). Az egymáshoz illeszkedő lap-él párok kettős összeszámolásából
| \(\displaystyle d_1+\ldots+d_L = 2E. \) | (2) |
A lapok szögeinek összegét is kiszámítjuk - kétféleképpen. A \(\displaystyle k\)-adik lapnak \(\displaystyle d_k\) éle van, így szögeinek összege \(\displaystyle (d_k-2)\cdot 180^\circ\). Másrészt, a feltétel szerint a szögek összege minden csúcsnál pontosan \(\displaystyle 180^\circ\). Tehát az összes szög összege
\(\displaystyle (d_1-2)\cdot180^\circ+(d_2-2)\cdot180^\circ+\ldots+(d_L-2)\cdot180^\circ = C\cdot180^\circ, \)
\(\displaystyle (d_1+d_2+\ldots+d_L) - 2L = C. \)
(2)-t, majd (1)-et behelyettesítve:
\(\displaystyle 2E-2L = C ,\)
\(\displaystyle 2(L+C-2)-2L=C, \)
\(\displaystyle 2C-4=C, \)
\(\displaystyle C=4. \)
A poliédernek tehát \(\displaystyle 4\) csúcsa van, ami csak úgy lehet, ha a test egy tetraéder.
II. Legyen a négy csúcs \(\displaystyle A,B,C,D\), és terítsük a tetraéder lapjait az \(\displaystyle ABC\) síkba az ábrán látható módon. Ekkor a \(\displaystyle BCD_1\), \(\displaystyle CAD_2\), \(\displaystyle ABD_3\) háromszögek rendre egybevágók a tetraéder \(\displaystyle BCD\), \(\displaystyle CAD\), \(\displaystyle ABD\) lapjaival.
Mivel a tetraéder csúcsai körül a szögek összege \(\displaystyle 180^\circ\),
\(\displaystyle D_2AC\angle + CAB\angle + BAD_3\angle = DAC\angle + CAB\angle + BAD\angle = 180^\circ, \)
és így az \(\displaystyle A,D_2,D_3\) pontok egy egyenesre esnek. Továbbá \(\displaystyle AD_2=AD=AD_3\), vagyis az \(\displaystyle A\) pont a \(\displaystyle D_2D_3\) szakasz felezőpontja. Hasonlóan, \(\displaystyle B\) a \(\displaystyle D_1D_3\), \(\displaystyle C\) pedig a \(\displaystyle D_1D_2\) szakasz felezőpontja.
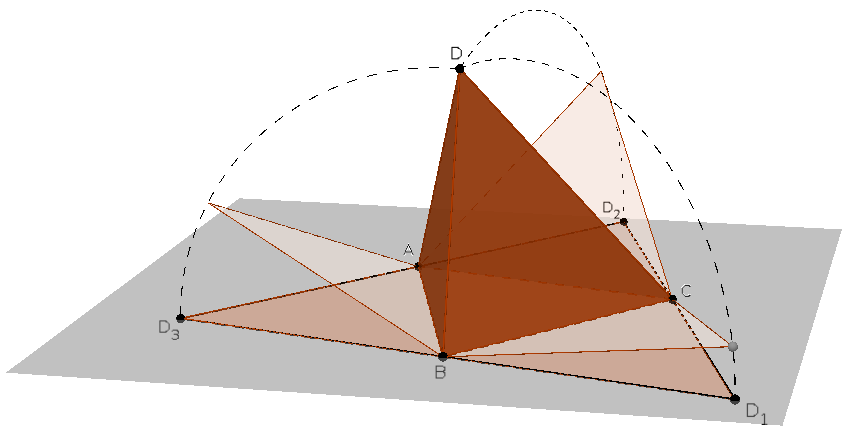
A \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) szakaszok a \(\displaystyle D_1D_2D_3\) háromszög középvonalai, amelyek a háromszöget négy egybevágó háromszögre osztják. Ezért a tetraéder lapjai is egybevágó háromszögek, és a szemközti élek egyenlő hosszúságúak: \(\displaystyle AB=CD_1=CD\), \(\displaystyle BC=AD_2=AD\) és \(\displaystyle CA=BD_3=BD\).
Statisztika:
54 dolgozat érkezett. 6 pontot kapott: Baran Zsuzsanna, Bodolai Előd, Borbényi Márton, Bukva Balázs, Cseh Kristóf, Csertán András, Döbröntei Dávid Bence, Fuisz Gábor, Gáspár Attila, Glasznova Maja, Horváth András János, Imolay András, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kovács 246 Benedek, Kővári Péter Viktor, Lajkó Kálmán, Márton Dénes, Matolcsi Dávid, Molnár-Sáska Zoltán, Nagy Dávid Paszkál, Nagy Kartal, Nagy Nándor, Németh 123 Balázs, Sal Kristóf, Schrettner Bálint, Schrettner Jakab, Szabó 417 Dávid, Szakály Marcell, Tóth Viktor, Váli Benedek, Vankó Miléna, Záhorský Ákos, Zólomy Kristóf. 5 pontot kapott: Busa 423 Máté, Dobák Dávid, Kasó Ferenc, Radnai Bálint, Szemerédi Levente, Varga-Umbrich Eszter. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2016. januári matematika feladatai
