 |
A B. 4778. feladat (2016. március) |
B. 4778. Legyen \(\displaystyle D\) az \(\displaystyle ABC\) hegyesszögű háromszög belső pontja. Szerkesszük meg az \(\displaystyle AD\), \(\displaystyle BD\) és \(\displaystyle CD\) átmérőjű köröket, majd húzzunk az \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) pontok mindegyikéből egy-egy érintőt az adott pontot nem tartalmazó két körhöz. Bizonyítsuk be, hogy a hat érintőszakasz négyzetének összege egyenlő a háromszög oldalainak négyzetösszegével.
(3 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
I. megoldás (vázlat). A körök páronként a háromszög \(\displaystyle AB\), \(\displaystyle BC\) és \(\displaystyle CA\) oldalakon lévő \(\displaystyle M\), \(\displaystyle N\) és \(\displaystyle P\) pontokban metszik egymást, \(\displaystyle DM\perp AB\), \(\displaystyle DN\perp BC\), \(\displaystyle DP\perp AC\) (Thalész-tétel). Legyenek \(\displaystyle E\), \(\displaystyle F\) és \(\displaystyle G\) az 1. ábrán látható érintési pontok. Ekkor a szelőszakaszok tételét felhasználva:
\(\displaystyle AE^2={AM}\cdot {AB}=({AD}+{DM})\cdot {AB} ={AD}\cdot {AB}.\)
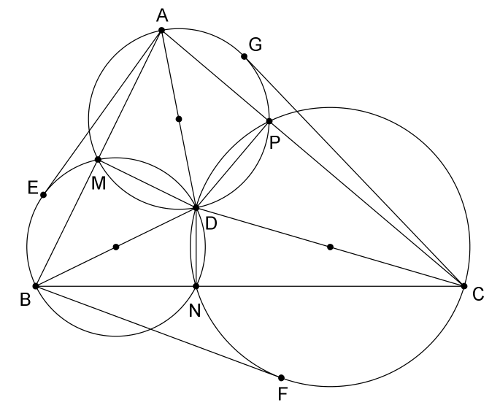
1. ábra
Hasonlóan: \(\displaystyle BF^2={BD}\cdot{BC}\) és \(\displaystyle CG^2={CD}\cdot{CA}={DC}\cdot{AC}\).
Így
\(\displaystyle 2(AE^2+BF^2+CG^2)=2({AD}\cdot{AB} +{BD}\cdot{BC}+{DC}\cdot{AC})=\)
\(\displaystyle =2[{AD}\cdot{AB}+{BD}\cdot{BC}+{DC}({ AB}+{BC})]=2[({AD}+{DC} ){AB}+({BD}+{DC}){BC}]=\)
\(\displaystyle =2({AC}\cdot{AB}+{BC}\cdot{BC})=2{AC}\cdot{AB}+2BC^2.\)
A \(\displaystyle {BC}={AC}-{AB}\) egyenletet négyzetre emelve:
\(\displaystyle BC^2=AC^2-2{AC}\cdot{AB}+AB^2,\)
amiből
\(\displaystyle 2{AC}\cdot{AB}= AC^2+AB^2-BC^2.\)
Ezt behelyettesítve előző eredményünkbe:
\(\displaystyle 2(AE^2+BF^2+CG^2 )=2{AC}\cdot{AB}+ 2BC^2=AC^2+AB^2-BC^2+2BC^2 =AC^2+AB^2+BC^2=b^2+c^2+a^2.\)
Ez hasonlóan belátható a másik három érintőszakasz négyzetösszegére.
II. megoldás (vázlat). A 2. ábra jelöléseit használva írjuk fel a \(\displaystyle CGK\) háromszögben a Pitagorasz-tételt, majd a \(\displaystyle CKD\) háromszögben a koszinusztételt:
\(\displaystyle g^2+r_a^2=CK^2\) és \(\displaystyle CK^2=r_a^2+4r_c^2-4r_a r_c \cos\beta\), amiből \(\displaystyle g^2=4r_c^2-4r_a r_c \cos\beta\).
Hasonlóan a \(\displaystyle BFM\) és \(\displaystyle BMD\) háromszögekben:
\(\displaystyle f^2+r_c^2=BM^2\) és \(\displaystyle BM^2=r_c^2+4r_b^2-4r_b r_c \cos\alpha\),
\(\displaystyle f^2=4r_b^2-4r_b r_c \cos\alpha\).
Majd végül az \(\displaystyle AEL\) és \(\displaystyle ALD\) háromszögekben:
\(\displaystyle e^2+r_b^2=AL^2\) és \(\displaystyle AL^2=r_b^2+4r_a^2-4r_a r_b \cos\gamma\),
\(\displaystyle e^2=4r_a^2-4r_a r_b \cos\gamma\).
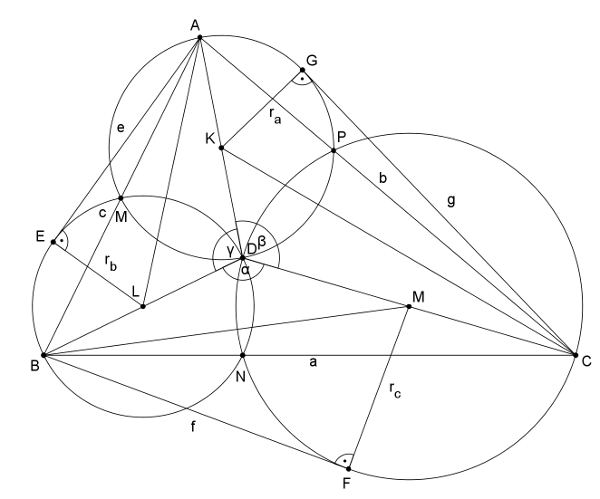
2. ábra
Összeadva a kapott egyenleteket:
\(\displaystyle e^2+f^2+g^2=4r_a^2+4r_b^2+4r_c^2-4r_a r_b \cos\gamma-4r_a r_c \cos\beta-4r_b r_c \cos\alpha.\)
A \(\displaystyle BCD\), \(\displaystyle ACD\) és \(\displaystyle ABD\) háromszögekben felírva a koszinusztételt és összeadva:
\(\displaystyle a^2+b^2+c^2=\)
\(\displaystyle =4r_b^2+4r_c^2-8r_b r_c \cos\alpha+4r_a^2+4r_c^2-8r_a r_c \cos\beta+4r_a^2+4r_c^2-8r_a r_b \cos\gamma=\)
\(\displaystyle =8r_a^2+8r_b^2+8r_c^2-8r_a r_b \cos\gamma-8r_a r_c \cos\beta-8r_b r_c \cos\alpha.\)
Összehasonlítva az előző egyenlettel látható, hogy
\(\displaystyle e^2+f^2+g^2=\frac{a^2+b^2+c^2}{2}.\)
Hasonlóan járhatunk el a másik három érintő esetében és négyzetösszegük ott is a háromszög oldalak négyzetösszegének felét adja.
Statisztika:
99 dolgozat érkezett. 3 pontot kapott: 89 versenyző. 2 pontot kapott: 9 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. márciusi matematika feladatai
