 |
A B. 4794. feladat (2016. április) |
B. 4794. Egy konvex poliéder lapjai közül legalább három ötszög. Legalább hány lapja van a poliédernek?
(5 pont)
A beküldési határidő 2016. május 10-én LEJÁRT.
1. megoldás. A feltételnek megfelelő, 7-lapú poliéder létezik, például egy háromoldalú hasáb egyik alaplapján az ábra szerint levágva a csúcsokat, olyan poliédert kapunk, amelynek három ötszög-, egy négyszög- és három háromszöglapja van.
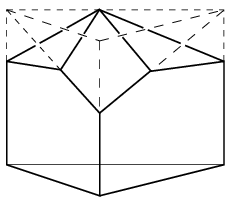
Megmutatjuk, hogy 6- vagy kevesebb lapú poliéder nem teljesítheti a feltételt.
Legyen a poliéder lapjainak, csúcsainak és éleinek száma \(\displaystyle L\), \(\displaystyle C\), illetve \(\displaystyle E\). Az Euler-féle poliédertétel szerint
\(\displaystyle L+C=E+2. \)
Minden csúcsból legalább három él indul ki, és minden él két csúcsot köt össze. Az egymáshoz kapcsolódó csúcs-él párok kettős összeszámolásából
\(\displaystyle 2E \ge 3C. \)
Most számoljuk össze az ötszöglapok csúcsait. Az első ötszöglapnak 5 csúcsa van. Bármely két lapnak legfeljebb 2 közös csúcsa van, így a második ötszöglapnak legalább 3 olyan csúcsa van, ami nem közös az első ötszöglappal. Hasonlóan, a harmadik ötszöglapnak legfeljebb \(\displaystyle 2+2\) csúcsa közös az első két ötszöglap valamelyikével; legalább 1 csúcsot még nem számoltunk. A három ötszöglapnak tehát összesen legalább \(\displaystyle 5+3+1=9\) különböző csúcsa van, így
\(\displaystyle C \ge 9. \)
A kapott összefüggéseket felhasználva:
\(\displaystyle L = E+2-C \ge \frac32C+2-C = \frac{C}2+2 \ge \frac92+2 > 6. \)
Tehát a poliédernek több, mint 6 lapja van.
2. megoldás. Egy másik indoklást mutatunk arra, hogy a poliédernek nem lehet 7-nél kevesebb lapja.
6-nál kevesebb lap azért sem lehet, mert egy ötszöglaphoz még 5 másik lap csatlakozik.
Tegyük fel, hogy 6 lap van: \(\displaystyle A,B,C\) ötszög, \(\displaystyle D,E,F\) tetszőleges. Minden egyes ötszöglaphoz további 5 lapnak, vagyis az összes többi lapnak csatlakoznia kell, így \(\displaystyle A,B,C\) mindegyike szomszédos \(\displaystyle D,E,F\) mindegyikével. A lapok gráfja tehát tartalmazza az \(\displaystyle (A,B,C)\times(D,E,F)\) három ház-három kút részgráfot, ami viszont nem síkba rajzolható. Tehát a lapok száma nem lehet \(\displaystyle 6\) sem.
Statisztika:
57 dolgozat érkezett. 5 pontot kapott: Andó Angelika, Baran Zsuzsanna, Bodolai Előd, Borbényi Márton, Bukva Balázs, Cseh Kristóf, Döbröntei Dávid Bence, Fajszi Bulcsú, Fuisz Gábor, Gáspár Attila, Hansel Soma, Horváth András János, Imolay András, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kosztolányi Kata, Kőrösi Ákos, Kővári Péter Viktor, Matolcsi Dávid, Nagy Dávid Paszkál, Nagy Kartal, Nagy Nándor, Németh 123 Balázs, Németh 417 Tamás, Nguyen Viet Hung, Páli Petra, Polgár Márton, Saár Patrik, Schrettner Jakab, Souly Alexandra, Szabó 417 Dávid, Szemerédi Levente, Tóth Viktor, Váli Benedek, Vári-Kakas Andor, Várkonyi Dorka, Weisz Máté, Zólomy Kristóf. 4 pontot kapott: Berényi Richárd, Keresztes László, Pálfy Máté András, Varga-Umbrich Eszter, Volford Anita. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 5 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2016. áprilisi matematika feladatai
