A B. 4862. feladat (2017. március)

B. 4862. Az \(\displaystyle ABCDE\) konvex ötszög \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DE\), illetve \(\displaystyle EA\) oldalainak felezőpontjai rendre \(\displaystyle M\), \(\displaystyle N\), \(\displaystyle P\), \(\displaystyle Q\), illetve \(\displaystyle R\). Mutassuk meg, hogy ha az \(\displaystyle AP\), \(\displaystyle BQ\), \(\displaystyle CR\) és \(\displaystyle DM\) szakaszok egy közös pontban metszik egymást, akkor ez a pont rajta van az \(\displaystyle EN\) szakaszon is.

Róka Sándor (Nyíregyháza)

(5 pont)

A beküldési határidő 2017. április 10-én LEJÁRT.

Megoldás:

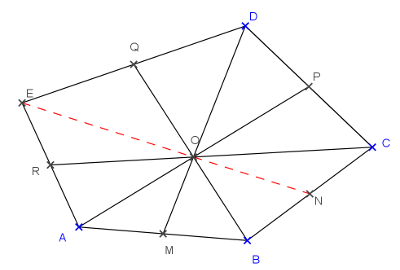
A közös metszéspont legyen \(\displaystyle O\). Az \(\displaystyle O\)-ból az \(\displaystyle A\)-ba vezető vektort jelölje \(\displaystyle \underline{a}\), és hasonló a többi jelölés is. Mivel \(\displaystyle O\) rajta van az \(\displaystyle AP\) szakaszon, így a két vektor vektoriális szorzata nulla: \(\displaystyle \underline{a}\times \underline{p}=\underline{0}\). A \(\displaystyle CD\) szakasz felezőpontja \(\displaystyle P\), így

\(\displaystyle \underline{0}=\underline{a}\times \underline{p}=\underline{a}\times \frac{\underline{c}+\underline{d}}{2}=\frac{\underline{a}\times \underline{c}+\underline{a}\times \underline{d}}{2}.\)

A vektoriális szorzás tulajdonsága miatt tehát \(\displaystyle \underline{a}\times \underline{c}=\underline{d}\times \underline{a}\). Hasonlóan kapjuk, hogy \(\displaystyle \underline{b}\times \underline{d}=\underline{e}\times \underline{b}\), \(\displaystyle \underline{c}\times \underline{e}=\underline{a}\times \underline{c}\), \(\displaystyle \underline{d}\times \underline{a}=\underline{b}\times \underline{d}\). Ezekből egyenlőségeken át sorra haladva eljutunk az \(\displaystyle \underline{e}\times \underline{b}=\underline{c}\times \underline{e}\) következtetéshez, hiszen

\(\displaystyle \underline{e}\times \underline{b}=\underline{b}\times \underline{d}=\underline{d}\times \underline{a}=\underline{a}\times \underline{c}=\underline{c}\times \underline{e}.\)

A bizonyítandó állítás:

\(\displaystyle \underline{0}=\underline{e}\times \underline{n}=\underline{e}\times \frac{\underline{b}+\underline{c}}{2}=\frac{\underline{e}\times \underline{b}+\underline{e}\times \underline{c}}{2},\)

és ez valóban teljesül, mert előbb megállapítottuk az \(\displaystyle \underline{e}\times \underline{b}=\underline{c}\times \underline{e}\) egyenlőséget.

Megjegyzés. Elemi úton is célhoz lehet jutni. Ilyen megoldást majd a nyomtatott lapban fogunk közölni.

Statisztika:

33 dolgozat érkezett.
5 pontot kapott:	Baran Zsuzsanna, Borbényi Márton, Busa 423 Máté, Csiszár Zoltán, Fülöp Anna Tácia, Gáspár Attila, Győrffy Ágoston, Imolay András, Janzer Orsolya Lili, Kerekes Anna, Kővári Péter Viktor, Nagy Nándor, Schrettner Jakab, Szabó 417 Dávid, Szemerédi Levente, Tanács Viktória, Tóth Viktor, Tubak Dániel, Weisz Máté.
4 pontot kapott:	Döbröntei Dávid Bence, Kocsis Júlia, Laki 37 Dániel, Németh 123 Balázs, Szabó Kristóf, Török Ádám.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2017. márciusi matematika feladatai