 |
A B. 4893. feladat (2017. szeptember) |
B. 4893. Az \(\displaystyle ABC\) háromszögben \(\displaystyle AB\ne BC\). A \(\displaystyle B\) pontból induló szögfelező a háromszög \(\displaystyle AC\) oldalát a \(\displaystyle D\) pontban, körülírt körét pedig (a \(\displaystyle B\) ponton kívül) az \(\displaystyle E\) pontban metszi. A \(\displaystyle DE\) szakasz, mint átmérő fölé emelt kör a körülírt kört az \(\displaystyle E\), majd másodszor az \(\displaystyle E\)-től különböző \(\displaystyle F\) pontban metszi. Bizonyítsuk be, hogy a \(\displaystyle BF\) egyenest a \(\displaystyle BD\) tengelyre tükrözve az \(\displaystyle ABC\) háromszög súlyvonalát kapjuk.
(6 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldás. Az \(\displaystyle A\) és \(\displaystyle C\) pontok szerepe felcserélhető, így az állítást elég abban az esetben igazolnunk, ha \(\displaystyle AB<BC\).
Legyen \(\displaystyle M\) az \(\displaystyle AC\) szakasz felezőpontja; ekkor tehát \(\displaystyle BM\) a háromszög \(\displaystyle B\)-ből induló súlyvonala. Azt fogjuk megmutatni, hogy \(\displaystyle MBD\sphericalangle=DBF\sphericalangle\); ebből már következik, hogy a \(\displaystyle BM\) súlyvonal és a \(\displaystyle BF\) egyenes szimmetrikus a \(\displaystyle BE\) egyenesre.
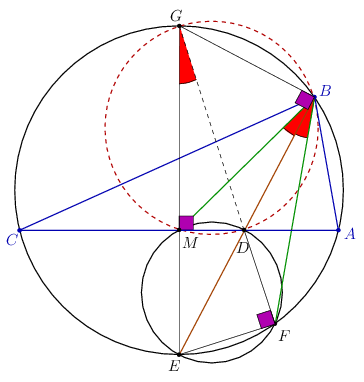
A háromszögben a \(\displaystyle BE\) szögfelező felezi körülírt kör \(\displaystyle B\)-vel szemközti \(\displaystyle AB\) ívét; az \(\displaystyle E\) pont tehát ennek a körívnek a felezőpontja. Az \(\displaystyle AC\) oldal felező merőlegese az \(\displaystyle EM\) egyenes; így az \(\displaystyle M\) pontból a \(\displaystyle DE\) szakasz derékszögben látszik, tehát a Thalész-tétel megfordítása szerint a \(\displaystyle DE\) átmérőjű kör az \(\displaystyle M\) ponton is átmegy.
Legyen \(\displaystyle G\) a körülírt körben a másik, \(\displaystyle B\)-t tartalmazó \(\displaystyle CA\) ív felezőpontja, amely szintén az \(\displaystyle AC\) oldal felező merőlegesén van. A körülírt körben \(\displaystyle EG\), a \(\displaystyle DEFM\) körben \(\displaystyle DE\) átmérő, ezért a Thalész-tétel szerint \(\displaystyle GFE\sphericalangle=90^\circ\), illetve \(\displaystyle DFE\sphericalangle=90^\circ\); A \(\displaystyle GF\) és a \(\displaystyle DF\) szakasz is merőleges \(\displaystyle EF\)-re, tehát a \(\displaystyle D\), \(\displaystyle F\) és \(\displaystyle G\) pontok egy egyenesen vannak.
Szintén a Thalész-tétel miatt a körülírt körben \(\displaystyle GBE\sphericalangle=90^\circ\). A \(\displaystyle BDMG\) négyszögnek az egymással szemközti \(\displaystyle B\) és \(\displaystyle M\) csúcsoknál derékszöge van, ezért \(\displaystyle BDMG\) húrnégyszög.
Végül a \(\displaystyle BDMG\), majd a \(\displaystyle BFEG\) húrnégyszögekben alkalmazva a kerületi szögek tételét láthatjuk, hogy
\(\displaystyle MBD\sphericalangle= MGD\sphericalangle= EGF\sphericalangle= EBF\sphericalangle= DBF\sphericalangle, \)
és ezt akartuk igazolni.
Statisztika:
53 dolgozat érkezett. 6 pontot kapott: Asztalos Ádám, Beke Csongor, Busa 423 Máté, Csépányi István, Csertán András, Csiszár Zoltán, Daróczi Sándor, Dobák Dániel, Döbröntei Dávid Bence, Fekete Richárd, Fuisz Gábor, Fülöp Anna Tácia, Gáspár Attila, Győrffy Ágoston, Harsányi Benedek, Janzer Orsolya Lili, Karácsony Márton, Kerekes Anna, Kovács Vince, Márton Dénes, Mikulás Zsófia, Molnár-Sáska Zoltán, Nagy Nándor, Nagymihály Panka, Nguyen Thac Bach, Noszály Áron, Pituk Gábor, Póta Balázs, Schrettner Jakab, Sulán Ádám, Szabó 417 Dávid, Szabó 864 Blanka, Szabó 997 Balázs István, Szabó Kristóf, Szemerédi Levente, Tiderenczl Dániel, Tubak Dániel, Várkonyi Zsombor, Velkey Vince, Weisz Máté, Zólomy Kristóf. 5 pontot kapott: Hoffmann Balázs, Kántor András Imre, Lukács Lilla Réka, Szécsényi Nándor. 4 pontot kapott: 2 versenyző. 3 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2017. szeptemberi matematika feladatai

