A B. 4958. feladat (2018. május)

B. 4958. Egy háromszög oldalai $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, a beírt kör sugara $\displaystyle r$, a köréírt kör sugara $\displaystyle R$. Bizonyítsuk be, hogy ha

$\displaystyle a+b+c =\frac{4}{rR} \quad\text{és}\quad \sqrt{ab}+\sqrt{bc}+\sqrt{ca} =6,$

akkor $\displaystyle R=2r$.

(Román versenyfeladat)

(4 pont)

A beküldési határidő 2018. június 11-én LEJÁRT.

Megoldás. Használjuk az 1. ábra jelöléseit. $\displaystyle T_{ABC}=T_{ABK}+T_{BCK}+T_{ACK}=\frac{a+b+c}{2}\cdot r$, valamint $\displaystyle T_{ABC}=\frac{ab\sin γ}{2}$.

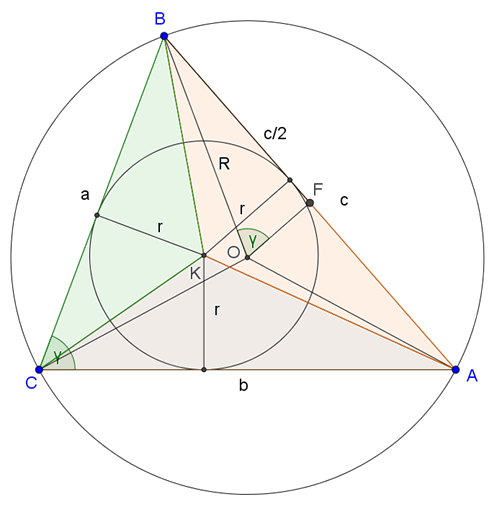
1. ábra

A $\displaystyle BFO$ derékszögű háromszögben $\displaystyle \frac c2=R\sin γ$. A feladat első egyenletéből:

$\displaystyle \frac{a+b+c}{2}\cdot rR=2,$

$\displaystyle T_{ABC}\cdot R=2,$

$\displaystyle \frac{ab\sin γ}{2}\cdot R=2,$

$\displaystyle \frac{ab}{2}\cdot R\sin γ=2,$

$\displaystyle \frac{ab}{2}\cdot\frac c2=2,$

$\displaystyle abc=8.$

Használjuk fel a számtani és mértani közép közötti összefüggést a második egyenlet jobb oldalának átalakítására:

$\displaystyle \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{3}≥\root 3\of {\sqrt{ab}\sqrt{bc}\sqrt{ca}} =\root 3\of {abc},$

$\displaystyle 6=\sqrt{ab}+\sqrt{bc}+\sqrt{ca}≥3\root 3\of {abc}=3\root 3\of 8=6.$

Ebből látszik, hogy a számtani és mértani közép egyenlő. Ez csak akkor lehetséges, ha $\displaystyle a=b=c$, vagyis a háromszög egyenlő oldalú (2. ábra)

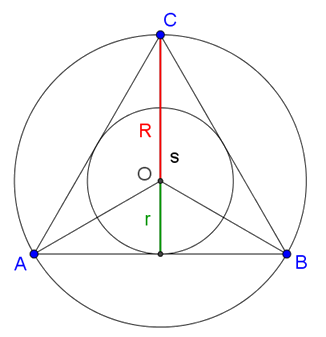
2. ábra

Ha egy egyenlő oldalú háromszögben s a súlyvonal hossza, akkor $\displaystyle R=\frac23 s$, $\displaystyle r=\frac13 s$, és így $\displaystyle R=2r$.

Statisztika:

68 dolgozat érkezett.
4 pontot kapott:	59 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2018. májusi matematika feladatai