A B. 5038. feladat (2019. szeptember)

B. 5038. Az $\displaystyle ABCDEFGH$ szabályos nyolcszög belsejében felvettünk egy $\displaystyle P$ pontot. Mutassuk meg, hogy az $\displaystyle ABP$, $\displaystyle CDP$, $\displaystyle EFP$ és $\displaystyle GHP$ háromszögek területeinek összege megegyezik a $\displaystyle BCP$, $\displaystyle DEP$, $\displaystyle FGP$ és $\displaystyle HAP$ háromszögek területeinek összegével.

(3 pont)

A beküldési határidő 2019. október 10-én LEJÁRT.

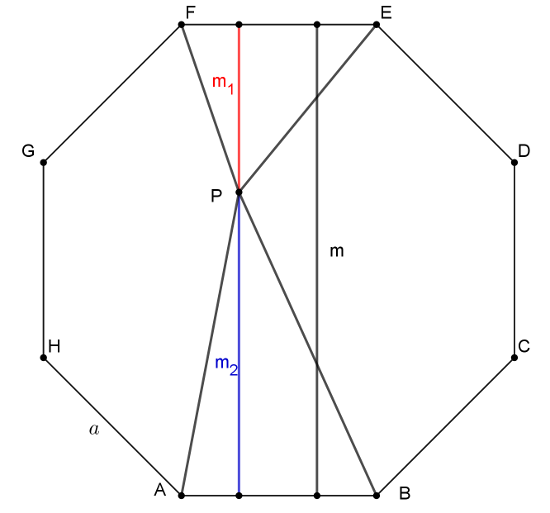
Megoldás. Ha $\displaystyle XY$ és $\displaystyle ZT$ a szabályos nyolcszög két, egymással szemköztes oldala, akkor e két oldalszakasz egymással párhuzamos és egyenlő. Ezért a $\displaystyle PXY$ és $\displaystyle PZT$ háromszögek $\displaystyle P$-ből induló magasságvonalai egy egyenesbe esnek, és a magasságok összege egyenlő az $\displaystyle XY$ és $\displaystyle ZT$ oldalak $\displaystyle m$ távolságával. Így – a nyolcszög oldalának hosszát $\displaystyle a$-val jelölve – a két háromszög területének összege:

$\displaystyle t_{PXY}+t_{PZT}=\frac{am_1}{2}+\frac{am_2}{2}=\frac{am}{2}.$

Tehát

$\displaystyle t_{PAB}+t_{PEF}=t_{PBC}+t_{PFG}=t_{PCD}+t_{PGH}=t_{PDE}+t_{PHA}(=\frac{am}{2}),$

amiből következik, hogy a $\displaystyle ABP$, $\displaystyle CDP$, $\displaystyle EFP$ és $\displaystyle GHP$ háromszögek területének összege, illetve a $\displaystyle BCP$, $\displaystyle DEP$, $\displaystyle FGP$ és $\displaystyle HAP$ háromszögek területének összege egyaránt $\displaystyle {am}$.

Statisztika:

203 dolgozat érkezett.
3 pontot kapott:	181 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2019. szeptemberi matematika feladatai