A B. 5044. feladat (2019. szeptember)

B. 5044. Adott az \(\displaystyle ABC\) háromszög \(\displaystyle AB\) oldalának belsejében a \(\displaystyle D\), az \(\displaystyle AC\) oldal belsejében az \(\displaystyle E\) pont; a \(\displaystyle BE\) és \(\displaystyle CD\) szakaszok metszéspontja \(\displaystyle M\). A \(\displaystyle BCM\) háromszög területe legyen \(\displaystyle x\), az \(\displaystyle EDM\) háromszög területe pedig \(\displaystyle y\). Igazoljuk, hogy

\(\displaystyle T_{ABC}\ge x \frac{\sqrt x+\sqrt y}{\sqrt x-\sqrt y}. \)

(6 pont)

A beküldési határidő 2019. október 10-én LEJÁRT.

1. megoldás.

Legyen \(\displaystyle p,q\in (0,1)\) úgy, hogy \(\displaystyle AD\colon DB=p\colon (1-p)\), \(\displaystyle AE\colon EC=q\colon (1-q)\), és az általánosság megszorítása nélkül tegyük fel, hogy \(\displaystyle T_{ABC}=1\). Írjuk fel az \(\displaystyle ADC\triangle\)-re és a \(\displaystyle BE\) egyenesre a Menelaosz-tételt (az irányítást figyelmen kívül hagyva):

\(\displaystyle \frac{AB}{BD}\cdot \frac{DM}{MC}\cdot \frac{CE}{EA}=1.\)

A bevezetett jelölések szerint \(\displaystyle AB \colon BD= 1\colon (1-p)\) és \(\displaystyle CE \colon EA=(1-q) \colon q\), ezekből pedig \(\displaystyle DM\colon MC=q(1-p) \colon (1-q)\) adódik, s ugyanígy kiszámítható, hogy \(\displaystyle EM\colon MA= p(1-q)\colon (1-p)\).

Vegyük észre, hogy a \(\displaystyle BCM\) és \(\displaystyle BCD\) háromszögek \(\displaystyle B\) csúcsból induló magassága közös, ezért \(\displaystyle T_{BCM}\colon T_{BCD}=CM \colon CD\); s hasonlóan a \(\displaystyle BCD\) és \(\displaystyle ABC\) háromszögek \(\displaystyle C\)-ből induló magassága közös, ezért \(\displaystyle T_{BCD}\colon T_{ABC}=BD \colon BA\). Felhasználva ezeket, a \(\displaystyle T_{ABC}=1\) feltevést, valamint a \(\displaystyle DM\colon MC=q(1-p) \colon (1-q)\) összefüggésből következő \(\displaystyle MC\colon DC = (1-q) \colon (1-pq)\) arányt kapjuk, hogy:

\(\displaystyle x=T_{BCD} \cdot \frac{MC}{DC}=T_{ABC}\cdot \frac{DB}{AB} \cdot \frac{MC}{DC}=(1-p)\cdot \frac{1-q}{1-pq}=\frac{(1-p)(1-q)}{1-pq}.\)

Másrészről bevezetve a \(\displaystyle \mu=DME\angle=CMB\angle\) jelölést:

\(\displaystyle \frac yx=\frac{2y}{2x}=\frac{ME\cdot MD \cdot \sin \mu}{MB \cdot MC \cdot \sin \mu }=\frac {DM}{MC}\cdot \frac{EM}{MB} =\frac{q(1-p)}{1-q}\cdot \frac{p(1-q)}{1-p}=pq.\)

A kapott összefüggéseket beírva, az igazolandó a következő alakot ölti:

\(\displaystyle 1\geq x \dfrac{\sqrt x+\sqrt y}{\sqrt x-\sqrt y}= x \cdot \frac{1+\sqrt{y/x}}{1-\sqrt{y/x}}=\frac{(1-p)(1-q)}{1-pq}\cdot \frac{1+\sqrt{pq}}{1-\sqrt{pq}},\)

ahol \(\displaystyle p,q\in (0,1).\) A kapott kifejezést egyszerűsítsük \(\displaystyle (1+\sqrt{pq})\)-val, majd alkalmazzuk a \(\displaystyle p+q\geq 2\sqrt{pq}\) számtani-mértani közép egyenlőtlenséget:

\(\displaystyle \frac{(1-p)(1-q)}{1-pq}\cdot \frac{1+\sqrt{pq}}{1-\sqrt{pq}}=\frac{(1-p)(1-q)}{(1-\sqrt{pq})^2}=\frac{1-p-q+pq}{1-2\sqrt{pq}+pq}\le \frac{1-2\sqrt{pq}+pq}{1-2\sqrt{pq}+pq}= 1.\)

Ezzel az állítást beláttuk. Egyenlőség pontosan akkor van, amikor a használt számtani-mértani közép egyenlőtlenségben is, azaz \(\displaystyle p=q\) esetén. A párhuzamos szelők tétele szerint ez pontosan \(\displaystyle DE\parallel BC\) esetén teljesül.

2. megoldás. Legyen \(\displaystyle P=AM\cap BC\), \(\displaystyle Q=AM\cap DE\), \(\displaystyle t=T_{ABC}\), \(\displaystyle b=T_{BMD}\) és \(\displaystyle c=T_{CME}\).

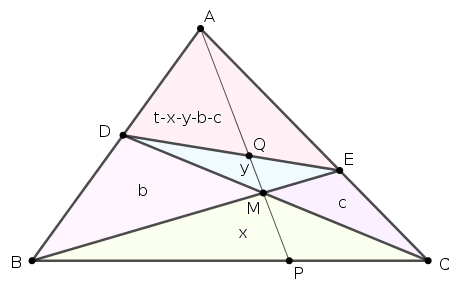
Az \(\displaystyle (AMPQ)\) négyes harmonikus, ezért

\(\displaystyle 1 = \frac{AQ}{MQ}\cdot\frac{MP}{AP} = \frac{T_{DEA}}{T_{DEM}}\cdot\frac{T_{BCM}}{T_{BCA}} = \frac{t-x-y-b-c}{y}\cdot\frac{x}{t}; \)

rendezve

\(\displaystyle (x-y) t = x(x+y+b+c). \)

(Az is látszik, hogy \(\displaystyle x>y\).)

A \(\displaystyle BCED\) négyszögben a szemközti háromszögek területének szorzata egyenlő, \(\displaystyle bc=xy\); a számtani és mértani közepek közötti egyenlőtlenségből \(\displaystyle b+c\ge2\sqrt{bc}=2\sqrt{xy}\), ezért

\(\displaystyle t = \frac{x(x+y+b+c)}{x-y} \ge \frac{x(x+y+2\sqrt{xy})}{x-y} = \frac{x\big(\sqrt{x}+\sqrt{y}\big)^2}{\big(\sqrt{x}+\sqrt{y}\big)\big(\sqrt{x}-\sqrt{y}\big)} = \frac{x\big(\sqrt{x}+\sqrt{y}\big)}{\sqrt{x}-\sqrt{y}}. \)

Akkor van egyenlőség, ha \(\displaystyle b=c\), vagyis ha \(\displaystyle DE\big\|BC\).

Statisztika:

21 dolgozat érkezett.
6 pontot kapott:	Andó Viola, Bán-Szabó Áron, Beke Csongor, Czett Mátyás, Füredi Erik Benjámin, Geretovszky Anna, Hámori Janka, Jánosik Áron, Kerekes Boldizsár, Lengyel Ádám, Molnár Lehel, Nguyen Bich Diep, Rareș Polenciuc, Somogyi Dalma, Tiderenczl Dániel, Vágó Bendegúz Zsolt.
5 pontot kapott:	Hegedűs Dániel.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2019. szeptemberi matematika feladatai