A B. 5057. feladat (2019. november)

B. 5057. Az \(\displaystyle AB\) átfogójú derékszögű háromszög \(\displaystyle BC\) befogóján vegyük fel a \(\displaystyle D\) és \(\displaystyle E\) pontokat úgy, hogy \(\displaystyle DAC\sphericalangle= EAD\sphericalangle= BAE\sphericalangle\). A \(\displaystyle C\) csúcsból az \(\displaystyle AD\) szakaszra, a \(\displaystyle D\) pontból az \(\displaystyle AB\) átfogóra bocsátott merőleges talppontjai rendre \(\displaystyle F\) és \(\displaystyle K\). Az \(\displaystyle AE\) szakaszt a \(\displaystyle CK\) egyenes a \(\displaystyle H\) pontban, a \(\displaystyle H\) ponton keresztül az \(\displaystyle AD\)-vel húzott párhuzamos a \(\displaystyle BC\) szakaszt az \(\displaystyle M\) pontban metszi. Mutassuk meg, hogy a \(\displaystyle CHM\) háromszög körülírt körének középpontja az \(\displaystyle F\) pont.

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2019. december 10-én LEJÁRT.

Megoldás.

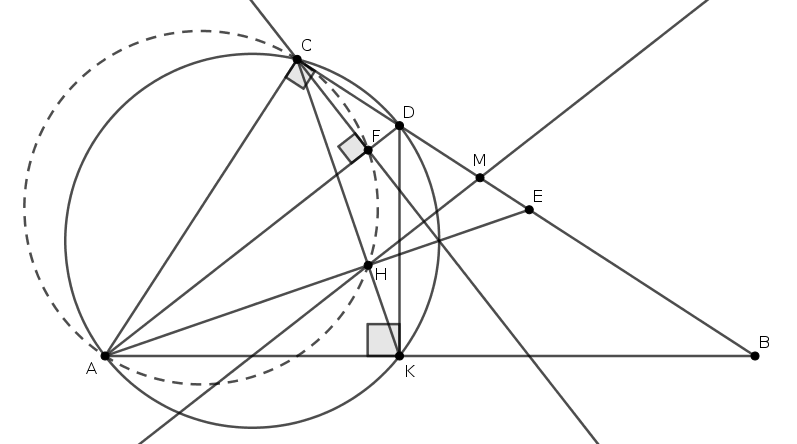
Használjuk az ábra jelöléseit.

A szögharmadolás miatt \(\displaystyle KAD\angle=2\alpha/3\), így \(\displaystyle ADK\angle=90^\circ-2\alpha/3\). Az \(\displaystyle AKDC\) húrnégyszög, mivel \(\displaystyle C\)-nél és \(\displaystyle K\)-nál, két szemközti csúcsánál derékszöge van, így az \(\displaystyle AK\) szakasz látószöge a \(\displaystyle C\) és \(\displaystyle D\) pontokból megegyezik, azaz \(\displaystyle ACK\angle=ADK\angle=90^\circ-2\alpha/3\). Ebből, mivel \(\displaystyle C\angle\) is derékszög, \(\displaystyle KCB\angle=2\alpha/3\) következik. Másrészt az \(\displaystyle ADC\) derékszögű háromszögben a szögharmadolás miatt \(\displaystyle DAC\angle=\alpha/3\), ahonnan \(\displaystyle ADC\angle=90^\circ-\alpha/3\). Innen viszont a \(\displaystyle CFD\) derékszögű háromszögben \(\displaystyle FCD\angle=\alpha/3\) adódik, így \(\displaystyle FC\) szögfelező a \(\displaystyle CHM\) háromszögben, \(\displaystyle FCD\angle=FCH\angle=\alpha/3\), továbbá \(\displaystyle CF\perp AD\parallel HM\) miatt \(\displaystyle HMC\) egyenlőszárú, és \(\displaystyle FC\) a \(\displaystyle HM\) oldal felező merőlegese.

Továbbá, a fentiek szerint \(\displaystyle FAH\angle=FCA\angle=\alpha/3\), így \(\displaystyle CAHF\) is húrnégyszög, és \(\displaystyle CAF\angle=FAH\angle\) miatt \(\displaystyle F\) felezi a megfelelő \(\displaystyle CH\) ívet, ebből következően illeszkedik \(\displaystyle CH\) szakaszfelező merőlegesére.

Így \(\displaystyle F\) illeszkedik \(\displaystyle CHM\) két oldalfelező merőlegesére, azaz valóban \(\displaystyle CHM\) körülírt körének középpontja.

Statisztika:

52 dolgozat érkezett.
5 pontot kapott:	Al-Hag Máté Amin, Andó Viola, Arató Zita, Argay Zsolt, Asztalos Ádám, Bán-Szabó Áron, Beke Csongor, Bencsik Ádám, Biró 424 Ádám, Csizmadia Miklós, Csonka Illés, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Győrffi Ádám György, Hámori Janka, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács 129 Tamás, Kurucz Máté, Laki Anna, Lovas Márton, Mácsai Dániel, Mátravölgyi Bence, Mezey Dorottya, Mohay Lili Veronika, Molnár Lehel, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nguyen Bich Diep, Révész Máté, Somogyi Dalma, Szabó 991 Kornél, Sztranyák Gabriella, Szűcs 064 Tamás, Terjék András József, Tiderenczl Dániel, Velich Nóra.
4 pontot kapott:	Baski Bence, Kitschner Bernadett, Kocsis Anett, Móra Márton Barnabás, Osztényi József, Seres-Szabó Márton.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2019. novemberi matematika feladatai