 |
A B. 5058. feladat (2019. november) |
B. 5058. Az \(\displaystyle ABC\) háromszög belsejében vegyünk fel egy tetszőleges \(\displaystyle P\) pontot. Az \(\displaystyle AP\), \(\displaystyle BP\) és \(\displaystyle CP\) egyenesek a \(\displaystyle BC\), \(\displaystyle AC\), illetve \(\displaystyle AB\) oldalakat rendre \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) pontokban metszik. Igazoljuk, hogy
\(\displaystyle \frac{AP}{A_1P}\cdot\frac{BP}{B_1P}\cdot\frac{CP}{C_1P}\ge 8. \)
Javasolta: Németh László (Fonyód)
(4 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
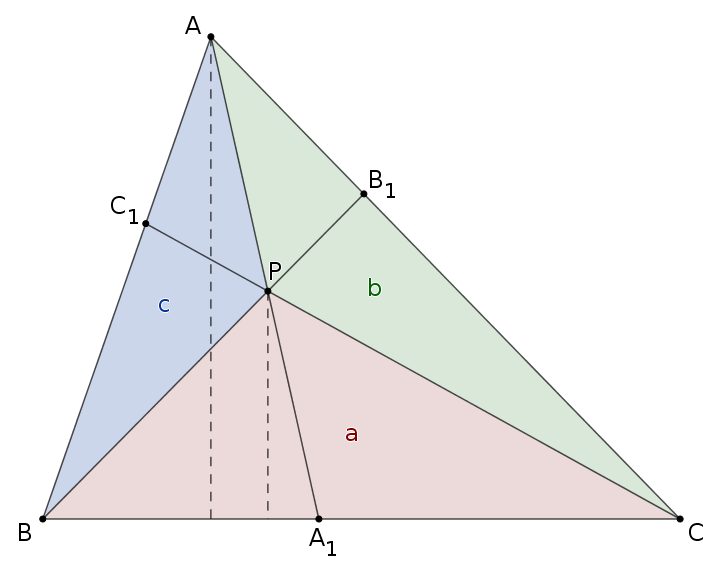
Megoldás. A \(\displaystyle PBC\), \(\displaystyle PCA\), \(\displaystyle PBA\) háromszögek területe legyen rendre \(\displaystyle a\), \(\displaystyle b\), illetve \(\displaystyle c\). Az \(\displaystyle ABC\) és a \(\displaystyle PBC\) háromszög \(\displaystyle BC\) oldala közös, az ehhez tartozó magasságok párhuzamosak, arányuk a párhuzamos szelők tétele miatt \(\displaystyle A_1A:A_1P\). Ezért
\(\displaystyle \frac{A_1A}{A_1P} = \frac{T_{ABC}}{T_{PBC}}. \)
Figyelembe véve, hogy \(\displaystyle A_1A=A_1P+AP\), \(\displaystyle T_{PBC}=a\) és \(\displaystyle T_{ABC}=a+b+c\),
\(\displaystyle \frac{A_1P+AP}{A_1P} = \frac{a+b+c}{a}; \)
mindkét oldalból \(\displaystyle 1\)-et kivonva
\(\displaystyle \frac{AP}{A_1P} = \frac{b+c}{a}. \)
A betűzés ciklikus cseréjével, ugyanígy kapjuk, hogy
\(\displaystyle \frac{BP}{B_1P} = \frac{c+a}{b} \quad\text{és}\quad \frac{CP}{C_1P} = \frac{a+b}{c}. \)
A kapott azonosságokat behelyettesítve, a feladat állítása a következő egyenlőtlenséggel ekvivalens:
| \(\displaystyle \frac{b+c}{a} \cdot \frac{c+a}{b} \cdot \frac{a+b}{c} \ge 8. \) | \(\displaystyle (1) \) |
Az (1) egyenlőtlenséget úgy igazoljuk, hogy a baloldalon mindhárom tört számlálóját alulról becsüljük a számtani és mértani közepek közötti egyenlőtlenséggel:
\(\displaystyle \frac{b+c}{a} \cdot \frac{c+a}{b} \cdot \frac{a+b}{c} \ge \frac{2\sqrt{bc}}{a} \cdot \frac{2\sqrt{ca}}{b} \cdot \frac{2\sqrt{ab}}{c} = 8. \)
A becslésünkben akkor áll egyenlőség, ha mindhárom esetben egymással egyenlő számok közepeit hasonlítjuk össze, vagyis ha \(\displaystyle a=b=c\). Szintén a területek arányaiból látjuk, hogy
\(\displaystyle \frac{a}{b} = \frac{T_{PBC}}{T_{PCA}} = \frac{BC_1}{C_1A}; \)
az \(\displaystyle a=b\) feltétel tehát akkor teljesül, ha \(\displaystyle C_1\) az \(\displaystyle AB\) oldal felezőpontja. Ugyanígy, \(\displaystyle a=c\) és \(\displaystyle b=c\) akkor teljesül, ha \(\displaystyle B_1\) az \(\displaystyle AC\), illetve ha \(\displaystyle A_1\) a \(\displaystyle BC\) oldal felezőpontja. A feladat állításában tehát akkor áll egyenlőség, ha \(\displaystyle P\) az \(\displaystyle ABC\) háromszög súlypontja.
Statisztika:
67 dolgozat érkezett. 4 pontot kapott: 62 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2019. novemberi matematika feladatai

