 |
A B. 5071. feladat (2020. január) |
B. 5071. Legyen az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalának \(\displaystyle B\)-hez közelebbi harmadolópontja \(\displaystyle A_1\), a \(\displaystyle C\)-hez közelebbi harmadolópontja \(\displaystyle A_2\), a \(\displaystyle CA\) oldal \(\displaystyle C\)-hez közelebbi harmadolópontja \(\displaystyle B_1\), az \(\displaystyle A\)-hoz közelebbi harmadolópontja \(\displaystyle B_2\), végül az \(\displaystyle AB\) oldal \(\displaystyle A\)-hoz közelebbi harmadolópontja \(\displaystyle C_1\), a \(\displaystyle B\)-hez közelebbi harmadolópontja \(\displaystyle C_2\). Bizonyítsuk be, hogy az \(\displaystyle A_1B_1C_1\) és \(\displaystyle B_2C_2A_2\) háromszögek egybevágók és területük az \(\displaystyle ABC\) háromszög területének harmadával egyenlő.
Javasolta: Bíró Bálint (Eger)
(3 pont)
A beküldési határidő 2020. február 10-én LEJÁRT.
1. megoldás. Használjuk a szokásos jelöléseket, és az \(\displaystyle AC\) oldal felezőpontja legyen \(\displaystyle F\). Mivel \(\displaystyle A_1C=\frac23 BC\) és \(\displaystyle B_1C=\frac13 AC=\frac13\cdot2 FC=\frac23 FC\), ezért \(\displaystyle A_1B_1C\triangle\sim BFC\triangle\), hiszen két oldal arányában és az általuk közrezárt szögben megegyeznek. Mivel ennek a két oldalnak az egyenese egybeesik, ezért a harmadik oldaluk párhuzamos egymással: \(\displaystyle A_1B_1||BF\), és nyilvánvalóan \(\displaystyle A_1B_1=\frac23 BF\). Hasonlóan kapjuk, hogy \(\displaystyle C_2B_2||BF\) és \(\displaystyle C_2B_2=\frac23 BF\). Ebből egyrészt az \(\displaystyle A_1B_1\) szakasz párhuzamos és egyenlő a \(\displaystyle C_2B_2\) szakasszal, másrészt \(\displaystyle t_{A_1B_1C}=\left(\frac23\right)^2t_{BFC}=\frac49\cdot\frac12t_{ABC}=\frac29t_{ABC}\). Ugyanígy \(\displaystyle t_{AC_2B_2}=\frac29t_{ABC}\).
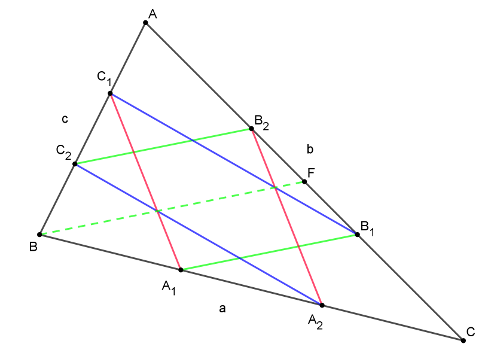
Hasonlóan kapjuk, hogy a \(\displaystyle B_1C_1\) szakasz párhuzamos és egyenlő az \(\displaystyle A_2C_2\) szakasszal, a \(\displaystyle C_1A_1\) szakasz párhuzamos és egyenlő a \(\displaystyle B_2A_2\) szakasszal, valamint \(\displaystyle t_{B_1AC_1}=t_{C_2BA_2}=t_{C_1BA_1}=t_{B_2A_2C}=\frac29t_{ABC}\).
Ezekből pedig egyrészt az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögek egybevágósága adódik, hiszen oldalaik páronként egyenlőek, másrészt területeikre
\(\displaystyle t_{A_2B_2C_2}=t_{A_1B_1C_1}=t_{ABC}-t_{A_1CB_1}-t_{C_1B_1A}-t_{A_1C_1B}=t_{ABC}-3\cdot \frac{2}{9}t_{ABC}= \frac{1}{3}t_{ABC}. \)
Ezzel mindkét bizonyítandó állítást beláttuk.
2. megoldás. Használjuk az ábra jelöléseit, az \(\displaystyle ABC\) háromszög szögei legyenek \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\) a szokásos módon. Az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögek egybevágóságát a megfelelő oldalaik egyenlőségével igazoljuk.
Először belátjuk, hogy \(\displaystyle A_1B_1=B_2C_2\). Ehhez írjuk fel a koszinusz-tételt az \(\displaystyle ABC\) háromszögben az \(\displaystyle \alpha\) és \(\displaystyle \gamma\) szögekre, ezekből
\(\displaystyle \cos \alpha=\frac{-a^2+b^2+c^2}{2bc} \quad \text{és} \quad \cos \gamma=\frac{a^2+b^2-c^2}{2ab}.\)
Most ismét a koszinusz-tételt alkalmazzuk az \(\displaystyle A_1B_1C\) háromszögben az \(\displaystyle A_1B_1\) oldalra. Kihasználjuk, hogy az \(\displaystyle A_1\) és \(\displaystyle B_1\) pontok választása miatt \(\displaystyle CA_1=2a/3\) és \(\displaystyle CB_1=b/3\). Így
$$\begin{align*} A_1B_1^2 &= CA_1^2 + CB_1^2 -2CA_1\cdot CB_1\cos \gamma = \frac{4}{9}a^2 + \frac{1}{9}b^2 -2\cdot \frac{2}{9}ab\frac{a^2+b^2-c^2}{2ab}= \\ &= \frac{4}{9}a^2+\frac{1}{9}b^2-\frac{2}{9}(a^2+b^2-c^2)= \frac{1}{9}(2a^2-b^2+2c^2). \end{align*}$$Másrészt felírhatjuk a koszinusz-tételt az \(\displaystyle AC_2B_2\) háromszögben a \(\displaystyle C_2B_2\) oldalra, és az előzőhöz hasonló számolással kapjuk, hogy
$$\begin{align*} B_2C_2^2&=AB_2^2+AC_2^2-2AB_2\cdot AC_2\cos \alpha = \frac{4}{9}c^2 + \frac{1}{9}b^2 -2\cdot \frac{2}{9}bc\frac{-a^2+b^2+c^2}{2bc}= \\ &= \frac{4}{9}c^2+\frac{1}{9}b^2-\frac{2}{9}(-a^2+b^2+c^2)= \frac{1}{9}(2a^2-b^2+2c^2). \end{align*}$$Nyertük, hogy \(\displaystyle A_1B_1^2=B_2C_2^2\), tehát \(\displaystyle A_1B_1=B_2C_2\). Ugyanígy látható be, hogy \(\displaystyle B_1C_1=C_2A_2\) és \(\displaystyle A_1C_1=B_2A_2\), amivel az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögek egybevágóságát beláttuk.
Statisztika:
110 dolgozat érkezett. 3 pontot kapott: 102 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. januári matematika feladatai

