A B. 5080. feladat (2020. február)

B. 5080. Az $\displaystyle ABC$ egyenlő szárú háromszög $\displaystyle AB$ alapjának felezőpontja $\displaystyle D$, $\displaystyle AC$ szárának $\displaystyle C$-hez közelebbi harmadolópontja $\displaystyle H$. A $\displaystyle BCH$ kör a $\displaystyle CD$ egyenest a $\displaystyle C$ és az $\displaystyle X$ pontban metszi. Mutassuk meg, hogy $\displaystyle CX=\frac 43r$, ahol $\displaystyle r$ az $\displaystyle ABC$ kör sugara.

(4 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Legyen a körülírt kör középpontja $\displaystyle O$, és a körülírt körön a $\displaystyle C$-vel átellenes pont $\displaystyle F$. Azt fogjuk igazolni, hogy $\displaystyle OX:OF=1:3$. Mivel $\displaystyle OC=OF=r$, ebből következik, hogy $\displaystyle CX=OC+OX=OC+\frac13OF=\frac43r$.

A kerületi és középponti szögek tételéből

$\displaystyle FOB\measuredangle = 2\cdot FCB\measuredangle = ACB\measuredangle,$

$\displaystyle BXC\measuredangle = BHC\measuredangle,$

továbbá

$\displaystyle BFC\measuredangle = BAC\measuredangle.$

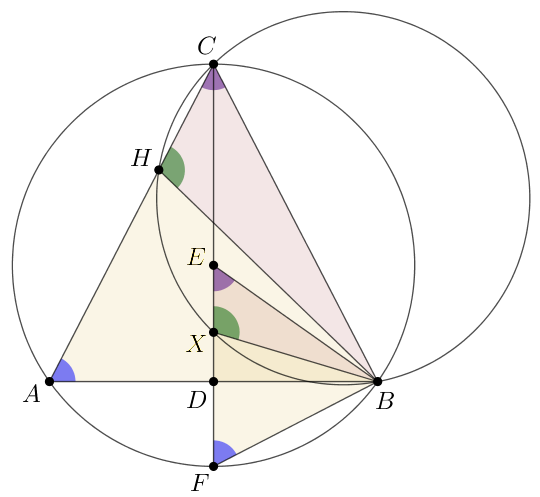
Az egyenlő szögekből látjuk, hogy $\displaystyle BCH\triangle\sim BOX\triangle$ és $\displaystyle ABC\triangle\sim FBO\triangle$. Ezért

$\displaystyle \frac{OX}{OF} = \frac{OX}{OB} \cdot \frac{OB}{OF} = \frac{CH}{CB} \cdot \frac{CB}{CA} = \frac{CH}{CA} = \frac13,$

és éppen ezt akartuk igazolni.

Megjegyzés. Annak, hogy $\displaystyle H$ éppen harmadolja a $\displaystyle CA$ szakaszt, a megoldás menete szempontjából nincs jelentősége; más $\displaystyle CH:CA$ arányok esetén is ugyanez a számolás működik, csak a kapott $\displaystyle CX:r$ arány lesz más.

Statisztika:

63 dolgozat érkezett.
4 pontot kapott:	57 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2020. februári matematika feladatai