A B. 5117. feladat (2020. szeptember)

B. 5117. Az $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$ pontok (ebben a sorrendben) egy egyenesre esnek. Az $\displaystyle AB$, $\displaystyle BC$ és $\displaystyle CD$ szakaszokra (azonos félsíkban) emelt szabályos háromszögek harmadik csúcsai legyenek rendre $\displaystyle E$, $\displaystyle F$, illetve $\displaystyle G$. Jelöljük az egyenesen szomszédos pontok távolságát a következőképpen: $\displaystyle AB=a$, $\displaystyle BC=b$, $\displaystyle CD=c$. Mutassuk meg, hogy az $\displaystyle EFG \sphericalangle $ akkor és csak akkor $\displaystyle 120^{\circ}$-os, ha $\displaystyle a+c=b$ vagy $\displaystyle \frac1a+\frac1c=\frac1b$.

(6 pont)

A beküldési határidő 2020. október 12-én LEJÁRT.

Megoldás. Az $\displaystyle a,b,c$ távolságok sorrendjétől függően három esetre bontjuk az állítást.

1. eset: Az $\displaystyle a,b,c$ távolságok közül $\displaystyle b$ a középső, azaz $\displaystyle a\le b\le c$ vagy $\displaystyle a\ge b\ge c$.

Az $\displaystyle A\leftrightarrow D$, $\displaystyle B\leftrightarrow C$, $\displaystyle E\leftrightarrow G$, $\displaystyle a\leftrightarrow c$ cserékkel az állítás önmagába megy át, de $\displaystyle a,b,c$ sorrendje megfordul. Ezért elég csak az $\displaystyle a\le b\le c$ esetet megvizsgálni.

A $\displaystyle BFE$ háromszögben $\displaystyle EBF\angle=60^\circ$. Mivel $\displaystyle BE=a\le BF=b$, és a nagyobb oldallal szemben nagyobb szög fekszik, $\displaystyle BFE\angle\le FEB\angle$; ebből azt kapjuk, hogy

$\displaystyle 0 < BFE\angle \le \frac{BFE\angle+FEB\angle}{2} = \frac{180^\circ-EBF\angle}{2} = 60^\circ. $

A $\displaystyle CGF$ háromszögben hasonlóan kapjuk, hogy

$\displaystyle 120^\circ=180^\circ-GCF\angle>GFC\angle \ge \frac{GFC\angle+CGF\angle}{2} = \frac{180^\circ-FCG\angle}{2} = 60^\circ. $

Ha az $\displaystyle EFG$ háromszög negatív körüljárású (1a. ábra), akkor

$\displaystyle EFG\angle = BFE\angle+CFB\angle+GFC\angle > 0+60^\circ+60^\circ = 120^\circ, $

tehát $\displaystyle EFG\angle=120^\circ$ nem lehetséges.

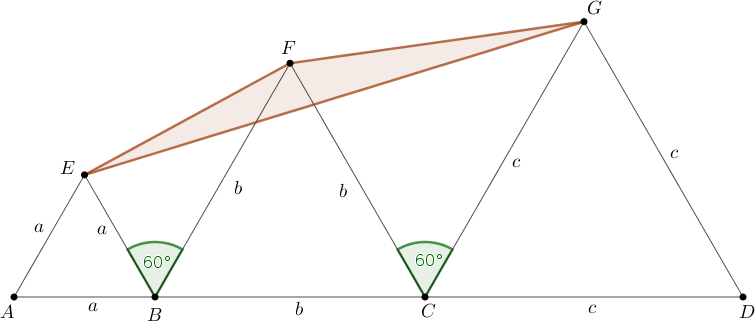
1a. ábra

Ha az $\displaystyle EFG$ háromszög pozitív körüljárású (1b. ábra), akkor

$\displaystyle EFG\angle = 360^\circ-BFE\angle-CFB\angle-GFC\angle > 360^\circ-60^\circ-60^\circ-120^\circ = 120^\circ, $

tehát $\displaystyle EFG\angle=120^\circ$ ilyenkor sem lehetséges.

1b. ábra

2. eset: Az $\displaystyle a,b,c$ távolságok közül $\displaystyle b$ a legnagyobb, azaz $\displaystyle b>a$ és $\displaystyle b>c$.

Húzzunk az $\displaystyle F$ ponton át párhuzamost az $\displaystyle ABCD$ egyenessel; ennek metszéspontja az $\displaystyle AE$ és $\displaystyle DG$ egyenesekkel legyen $\displaystyle P$, illetve $\displaystyle Q$. Az $\displaystyle ABFP$ és a $\displaystyle CDQF$ paralelogrammákból és az $\displaystyle ABE$, $\displaystyle BCF$, $\displaystyle CDG$ szabályos háromszögekből láthatjuk, hogy $\displaystyle FP=AB=a$, $\displaystyle FQ=CD=c$, $\displaystyle EP=AP-AE=BF-AB=b-a$ és $\displaystyle GQ=DQ-DG=CF-CD=b-c$. (2. ábra.)

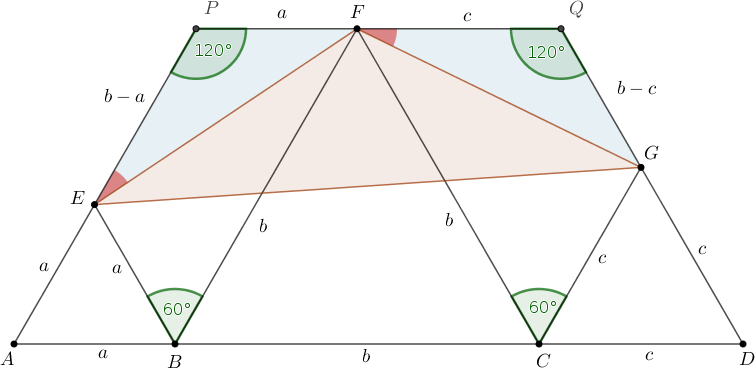
2. ábra

Az $\displaystyle EFP$ és $\displaystyle FGQ$ háromszögekben $\displaystyle FPE\angle=GQF\angle=120^\circ$. Ha $\displaystyle EFG\angle=120^\circ$, akkor a két háromszög szögeit összeszámolva

$\displaystyle PEF\angle = 180^\circ-FPE\angle-EFP\angle = 180^\circ-EFG\angle-EFP\angle = GFQ\angle; $

az $\displaystyle EFP$ és $\displaystyle FGQ$ háromszögek szögei megegyeznek, tehát a két háromszög hasonló egymáshoz. Megfordítva, ha a két háromszög hasonló, akkor

$\displaystyle EFG\angle = 180^\circ-EFP\angle-QFG\angle = 180^\circ-EFP\angle-PEF\angle = FPE\angle = 120^\circ. $

Tehát: $\displaystyle EFG\angle=120^\circ$ akkor és csak akkor teljesül, ha az $\displaystyle EFP$ és $\displaystyle FGQ$ háromszögek hasonlóak.

Mivel $\displaystyle FPE\angle=GQF\angle$, a hasonlóság azzal ekvivalens, hogy a közös szög melletti oldalak aránya egyenlő:

$$\begin{gather*} \frac{EP}{FP} = \frac{FQ}{GQ}, \\ \frac{b-a}{a} = \frac{c}{b-c}, \\ (b-a)(b-c) = ac, \\ b^2 = ab+cb, \\ b=a+c. \end{gather*}$$

Megfordítva, ha $\displaystyle b=a+c$, akkor $\displaystyle b>a$ és $\displaystyle b>c$, tehát valóban a 2. eset áll fenn, és az előbbi lépéseket visszafelé elmondva kapjuk, hogy az $\displaystyle EFP$ és $\displaystyle FGQ$ háromszögek hasonlóak, tehát $\displaystyle EFG\angle=120^\circ$.

3. eset: Az $\displaystyle a,b,c$ távolságok közül $\displaystyle b$ a legkisebb, azaz $\displaystyle b<a$ és $\displaystyle b<c$.

Húzzunk ismét az $\displaystyle F$ ponton át párhuzamost az $\displaystyle ABCD$ egyenessel; ennek metszéspontja a $\displaystyle BE$ és $\displaystyle CG$ szakaszokkal legyen $\displaystyle R$, illetve $\displaystyle S$. (3. ábra.)

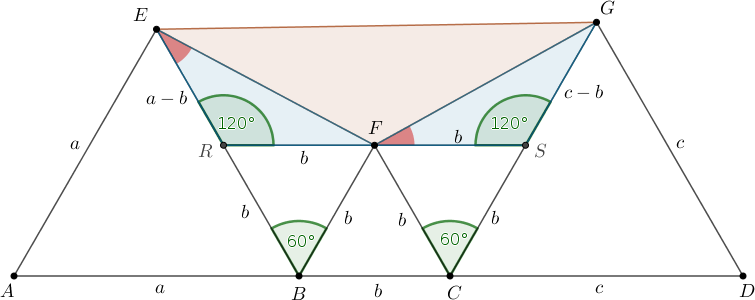
3. ábra

A 2. esethez hasonlóan látjuk, hogy $\displaystyle EFG\angle=120^\circ$ akkor és csak akkor teljesül, ha az $\displaystyle FER$ és $\displaystyle GFS$ háromszögek hasonlóak, aminek ekvivalens feltétele:

$$\begin{gather*} \frac{ER}{FR} = \frac{FS}{GS}, \\ \frac{a-b}{b} = \frac{b}{c-b}, \\ (a-b)(c-b) = b^2, \\ ac = ab + bc, \\ \frac1b = \frac1a+\frac1c. \end{gather*}$$

Megfordítva, ha $\displaystyle \frac1b = \frac1a+\frac1c$, akkor $\displaystyle \frac1b>\frac1a$ és $\displaystyle \frac1b>\frac1c$, vagyis $\displaystyle b<a$ és $\displaystyle b<c$, tehát valóban a 3. eset áll fenn; az előbbi számolás visszafelé elmondva igazolja, hogy az $\displaystyle FER$ és $\displaystyle GFS$ háromszögek hasonlóak, tehát $\displaystyle EFG\angle=120^\circ$.

Statisztika:

88 dolgozat érkezett.

6 pontot kapott: 56 versenyző.

5 pontot kapott: 17 versenyző.

3 pontot kapott: 1 versenyző.

2 pontot kapott: 5 versenyző.

1 pontot kapott: 6 versenyző.

0 pontot kapott: 1 versenyző.

Nem versenyszerű: 2 dolgozat.

A KöMaL 2020. szeptemberi matematika feladatai

88 dolgozat érkezett.
6 pontot kapott:	56 versenyző.
5 pontot kapott:	17 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

Már regisztráltál?
Új vendég vagy?