 |
A B. 5138. feladat (2020. december) |
B. 5138. Az \(\displaystyle ABC\) nem egyenlő szárú háromszög \(\displaystyle A\)-ból, illetve \(\displaystyle B\)-ből induló belső szögfelezője a szemközti oldalt az \(\displaystyle A'\), illetve \(\displaystyle B'\) pontban metszi. Bizonyítandó, hogy \(\displaystyle A'B'\) felezőmerőlegese akkor és csak akkor megy át a beírt kör középpontján, ha \(\displaystyle AB' + BA' = AB\).
Javasolta: Surányi László (Budapest)
(5 pont)
A beküldési határidő 2021. január 11-én LEJÁRT.
Megoldás. Azt fogjuk belátni, hogy nem egyenlő szárú háromszög esetén azok az állítások, hogy \(\displaystyle AB'+BA'=AB\), és \(\displaystyle A'B'\) felezőmerőlegese átmegy az \(\displaystyle O\) ponton egyaránt ekvivalensek azzal, hogy a háromszögnek a \(\displaystyle C\) csúcsnál \(\displaystyle 60^\circ\)-os szöge van.
Írjuk fel az algebrai feltételét annak, hogy \(\displaystyle AB'+BA'=AB\). A belső szögfelező a szemközti oldalt a szomszédos oldalak arányában osztja ketté, így a szokásos jelölések mellett az egyenlőség feltétele:
\(\displaystyle \frac{bc}{a+c}+\frac{ac}{b+c}=c.\)
Ekvivalens átalakításokkal:
\(\displaystyle \frac{b}{a+c}+\frac{a}{b+c}=1,\)
\(\displaystyle b^2+bc+a^2+ac=ab+bc+ac+c^2,\)
\(\displaystyle a^2-ab+b^2=c^2.\)
Ez a koszinusz-tétellel összevetve azt jelenti, hogy a háromszög \(\displaystyle AB\)-vel szemközti \(\displaystyle \gamma\) szöge \(\displaystyle 60^\circ\)-os. Itt a lépéseink megfordíthatóak, tehát \(\displaystyle AA'+BB'=AB\) akkor és csak akkor, ha \(\displaystyle \gamma=60^\circ\).
Most nézzük meg, mi a feltétele annak, hogy az \(\displaystyle A'B'\) szakasz felezőmerőlegese átmenjen a beírt kör \(\displaystyle O\) középpontján. Legyenek a beírt kör érintési pontjai rendre az \(\displaystyle AB, BC\) és \(\displaystyle CA\) oldalakon az \(\displaystyle E, F\) és \(\displaystyle G\) pontok. A feladat felttételei alapján tudjuk, hogy a háromszög nem egyenlő szárú, tehát a szögfelezők metszéspontjai nem esnek egybe a beírt kör érintési pontjaival.
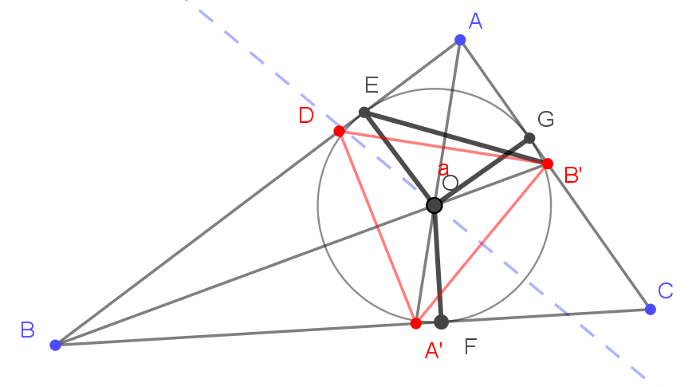
Ha az \(\displaystyle A'B'\) szakasz felezőmerőlegese átmegy az \(\displaystyle O\) ponton, akkor \(\displaystyle OA'=OB'\). Az \(\displaystyle O\) pont a beírt kör középpontja, így \(\displaystyle OF=OG=r\) is teljesül. Az \(\displaystyle OFA'\) és \(\displaystyle OGB'\) derékszögű háromszögeknek két-két oldala és a nagyobbikkal szemközti szöge megegyezik, tehát egybevágók. egyenlő tehát az \(\displaystyle OA'F\sphericalangle\) és az \(\displaystyle OB'G\sphericalangle\).
Számoljuk ki at \(\displaystyle OA'F\) szöget. Itt két eset lehetséges az \(\displaystyle ABA'\) háromszög szögeinek nagysága alapján, mivel az \(\displaystyle OA'F\) szög mindenképpen hegyesszög. Ha \(\displaystyle \beta+\frac{\alpha}{2}<90^\circ\), akkor az \(\displaystyle OA'F\sphericalangle\) az \(\displaystyle ABA'\) háromszög külső szöge, vagyis
\(\displaystyle OA'F\sphericalangle=\beta+\frac{\alpha}{2}.\)
Ha pedig \(\displaystyle \beta+\frac{\alpha}{2}>90^\circ\), akkor az \(\displaystyle OA'F\) szög az \(\displaystyle ABA'\) háromszög harmadik belső szöge:
\(\displaystyle OA'F\sphericalangle=180^\circ-\beta-\frac{\alpha}{2}=\gamma+\frac{\alpha}{2}.\)
Az \(\displaystyle OB'G\) háromszögnél hasonlóan kapjuk, hogy
\(\displaystyle OB'G\sphericalangle=\alpha+\frac{\beta}{2}~~\text{ vagy} ~~ OB'G\sphericalangle=\gamma+\frac{\beta}{2}.\)
Az \(\displaystyle OA'F\sphericalangle=OB'G\sphericalangle\) teljesüléséhez valamelyik párosításban egyenlőségnek kell teljesülnie. Ha \(\displaystyle \beta+\frac{\alpha}{2}=\alpha+\frac{\beta}{2}\) vagy \(\displaystyle \gamma+\frac{\alpha}{2}=\gamma+\frac{\beta}{2}\), akkor azt kapnánk, hogy \(\displaystyle \alpha=\beta\), ezt pedig most a feltétel miatt nem lehetséges. Marad az a további két lehetőség, hogy
\(\displaystyle \beta+\frac{\alpha}{2}=\gamma+\frac{\beta}{2}~~\text{ vagy } ~~ \alpha+\frac{\beta}{2}=\gamma+\frac{\alpha}{2}.\)
Mindkettőből rendezéssel:
\(\displaystyle \gamma=\frac{\alpha+\beta}{2},\)
\(\displaystyle 2\gamma=\alpha+\beta=180^\circ-\gamma,\)
\(\displaystyle \gamma=60^\circ.\)
Ha a háromszög nem egyenlő szárú, akkor ez utóbbi számolás lépései is megfordíthatóak.
Ezzel az állítást beláttuk.
Statisztika:
68 dolgozat érkezett. 5 pontot kapott: Arató Zita, Bán-Szabó Áron, Beinschroth Ninett, Bencsik Ádám, Bencsik Dávid, Biró 424 Ádám, Bognár 171 András Károly, Csizmadia Miklós, Diaconescu Tashi, Duchon Márton, Farkas 512 Izabella, Fekete Richárd, Győrffi Ádám György, Hegedűs Dániel, Horváth 530 Mihály, Jánosik Máté, Kalocsai Zoltán, Kelemen Anna, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács 129 Tamás, Kökényesi Márk Péter, Lengyel Ádám, Lovas Márton, Mohay Lili Veronika, Móricz Benjámin, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Páhán Anita Dalma, Rareș Polenciuc, Romaniuc Albert-Iulian, Sándor Péter, Seres-Szabó Márton, Simon László Bence, Sógor Bence, Somogyi Dalma, Szakács Ábel, Szanyi Attila, Sztranyák Gabriella, Török Ágoston, Varga Boldizsár, Velich Nóra, Virág Rudolf, Wiener Anna, Zömbik Barnabás. 4 pontot kapott: 8 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2020. decemberi matematika feladatai

