 |
A B. 5167. feladat (2021. április) |
B. 5167. Adott a síkon két kör úgy, hogy vannak közös belső érintőik. Mutassuk meg, hogy e közös érintők érintési pontjain átmenő kör középpontja felezi a két kör középpontjait összekötő szakaszt.
Javasolta: Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 8.C. osztály
(3 pont)
A beküldési határidő 2021. május 10-én LEJÁRT.
Megoldás. Legyen a két kör középpontja \(\displaystyle O_1\) és \(\displaystyle O_2\), a közös belső érintők érintési pontjai \(\displaystyle A, C\), illetve \(\displaystyle B, D\) az ábra szerint.
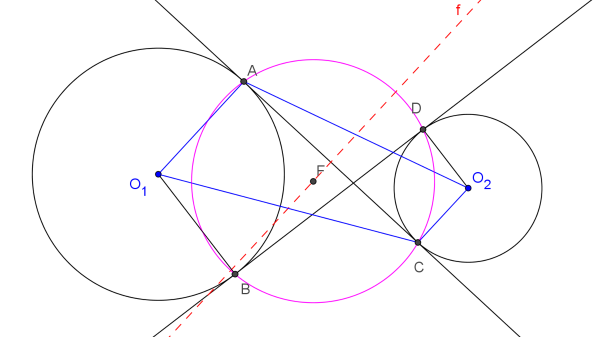
Az egész ábra szimmetrikus a centrálisra, így \(\displaystyle ABCD\) szimmetrikus trapéz, tehát írható köré kör, továbbá a kör középpontja rajta van a centrálison. Az \(\displaystyle AC\) érintőszakaszhoz tartozó \(\displaystyle O_1A\) és \(\displaystyle O_2C\) sugarak merőlegesek az érintőre, így egymással párhuzamosak. Az eddigiek alapján látjuk, hogy \(\displaystyle O_1AO_2C\) trapéz, melynek alapjai az \(\displaystyle O_1A\) és \(\displaystyle O_2C\) szakaszok, átlói pedig \(\displaystyle AC\) és \(\displaystyle O_1O_2\). Az érintési pontokon átmenő körnek \(\displaystyle AC\) az egyik húrja, így annak \(\displaystyle f\) felezőmerőlegese párhuzamos az alapokkal, felezi az átlót, tehát éppen a középvonal egyenese. Másrészt tudjuk, hogy a húr felezőmerőlegese átmegy a kör \(\displaystyle F\) középpontján. A középvonal felezi a másik átlót, az \(\displaystyle O_1O_2\) szakaszt is. Ezzel az állítást beláttuk.
Statisztika:
59 dolgozat érkezett. 3 pontot kapott: 52 versenyző. 2 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2021. áprilisi matematika feladatai

