 |
A B. 5346. feladat (2023. november) |
B. 5346. Mely \(\displaystyle n\)-ekre létezik olyan \(\displaystyle n\)-szög, amelynek oldalai egyenlő hosszúak, és minden oldala pontosan két másik oldalával párhuzamos?
Javasolta: Hujter Bálint (Budapest)
(5 pont)
A beküldési határidő 2023. december 11-én LEJÁRT.
Megoldás. Akkor és csak akkor létezik ilyen \(\displaystyle n\)-szög, ha \(\displaystyle 3 \mid n\) és \(\displaystyle n \geq 9\).
Egy a feltételeknek eleget tevő \(\displaystyle n\)-szögben minden oldal két másikkal párhuzamos, azaz az oldalak hármasával tartoznak egy-egy párhuzamossági osztályba, tehát \(\displaystyle 3 \mid n\) nyilvánvalóan szükséges feltétel.
\(\displaystyle n=3\) esetén mindhárom oldal párhuzamos kellene legyen, ez lehetetlen.
\(\displaystyle n=6\) esetén két párhuzamossági osztály van, azaz egy jó \(\displaystyle n\)-szöghöz megadható két vektor, \(\displaystyle \mathbf{a}\) és \(\displaystyle \mathbf{b}\) úgy, hogy mindegyik oldal párhuzamos és egyenlő hosszú valamelyikkel. Körüljárva a sokszöget, egy oldalon végigmenve \(\displaystyle \alpha_i \mathbf{a}\)-val vagy \(\displaystyle \beta_i \mathbf{b}\)-vel mozdulunk el, ahol \(\displaystyle \alpha_i,\beta_i \in \{-1,1\}\). Így egy teljes körüljárás során a teljes elmozdulásunk
\(\displaystyle (\alpha_1 + \alpha_2 + \alpha_3) \mathbf{a} + (\beta_1 + \beta_2 + \beta_3) \mathbf{b}. \)
Ez az összeg nullvektor kellene legyen, hiszen egy sokszögön jártunk körbe. Mivel \(\displaystyle \mathbf{a}\) és \(\displaystyle \mathbf{b}\) nem lehet párhuzamos, ez csak úgy lehet, ha mindkettejük együtthatója \(\displaystyle 0\). De \(\displaystyle \alpha_1 + \alpha_2 + \alpha_3\) nem lehet 0, hiszen 3 db \(\displaystyle \pm1\) összege csak \(\displaystyle -3\), \(\displaystyle -1\), \(\displaystyle 1\) vagy \(\displaystyle 3\) lehet.
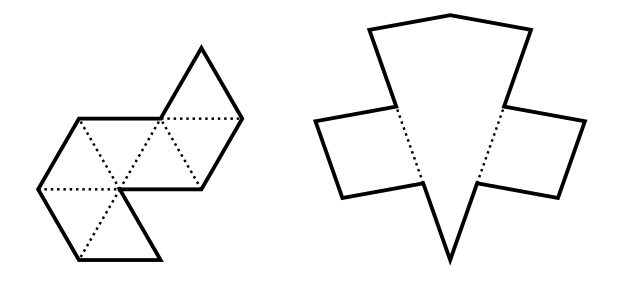
\(\displaystyle n = 9\) és \(\displaystyle n=12\) esetére mutatunk egy-egy egyedi konstrukciót. A 9-szöget 7 db egybevágó szabályos háromszögből ragasztottuk össze. A 12-szöget úgy kaptuk, hogy vettünk egy deltoidot \(\displaystyle 1\), \(\displaystyle 1\), \(\displaystyle 3\), \(\displaystyle 3\) oldalakkal, majd a hosszú oldalak középső harmadához hozzáragasztottunk egy-egy olyan rombuszt, amelynek 1 hosszú oldalai párhuzamosak a deltoid oldalaival.
Ha \(\displaystyle n \geq 15\) páratlan és 3-mal osztható, akkor \(\displaystyle k = n/3\) páratlan egész. Vegyük fel az \(\displaystyle A_1(0,0)\) és \(\displaystyle A_2(2,0)\) pontokat egy derékszögű koordináta-rendszerben, majd ezekre illesszük az \(\displaystyle A_1A_2 \ldots A_k\) szabályos \(\displaystyle k\)-szöget. Az \(\displaystyle A_i\) csúcsok közül a legnagyobb \(\displaystyle x\)-koordinátájú (legjobbrább levő) legyen \(\displaystyle A_p\), a legkisebb \(\displaystyle x\) koordinátájú (legbalrább levő) legyen \(\displaystyle A_q\). Mivel \(\displaystyle k \geq 5\), ezért \(\displaystyle 3 \leq p < q \leq k\), továbbá az \(\displaystyle A_1A_2\) felezőmerőlegesére vett szimmetria miatt \(\displaystyle A_p\) és \(\displaystyle A_q\) \(\displaystyle y\)-koordinátája megegyezik. (Könnyen ellenőrizhető, hogy mindig teljesül \(\displaystyle p+q= k+3\) is, bár ennek nincs jelentősége a későbbiekben).
Az \(\displaystyle A_1A_2 \ldots A_k\) szabályos \(\displaystyle k\)-szöget \(\displaystyle \overrightarrow{A_{q}A_{p}}\) vektorral eltolva kapjuk a \(\displaystyle B_1B_2 \ldots B_k\) szabályos \(\displaystyle k\)-szöget, ezt újra eltolva \(\displaystyle \overrightarrow{A_{q}A_{p}}\)-vel kapjuk a \(\displaystyle C_1C_2 \ldots C_k\) szabályos \(\displaystyle k\)-szöget. Így persze \(\displaystyle A_p = B_q\), \(\displaystyle B_p = C_q\); továbbá \(\displaystyle A_{p-1},A_{q+1},B_{p-1},B_{q+1},C_{p-1}\) és \(\displaystyle C_{q+1}\) pontok mind egy vízszintes (\(\displaystyle x\)-tengellyel párhuzamos) egyenesre esnek, ezt az egyenest jelölje \(\displaystyle t\). Tükrözve az \(\displaystyle A_3\) és \(\displaystyle B_3\) pontokat a \(\displaystyle t\) egyenesre kapjuk az \(\displaystyle A'_3\) és \(\displaystyle B'_3\) pontokat. Így az
$$\begin{eqnarray*} A_1 A_2 A_{p-1} A'_p B_{q+1} B_{q+2} \ldots B_k B_1 B_2 B_3 \ldots B_{p-1} B'_p C_{q+1} C_{q+2} \ldots C_k \\ C_1 C_2 \ldots C_{q-1} B_p B_{p+1} B_{p+2} \ldots B_{q-1} A_p A_{p+1} A_{p+2} \ldots A_{k-1} A_k \end{eqnarray*}$$sokszög éppen eleget tesz majd a feltételeknek, mivel 3-3 oldala áll a szabályos sokszög mindegyik oldalirányának megfelelően (és minden oldala egyenlő hosszú).
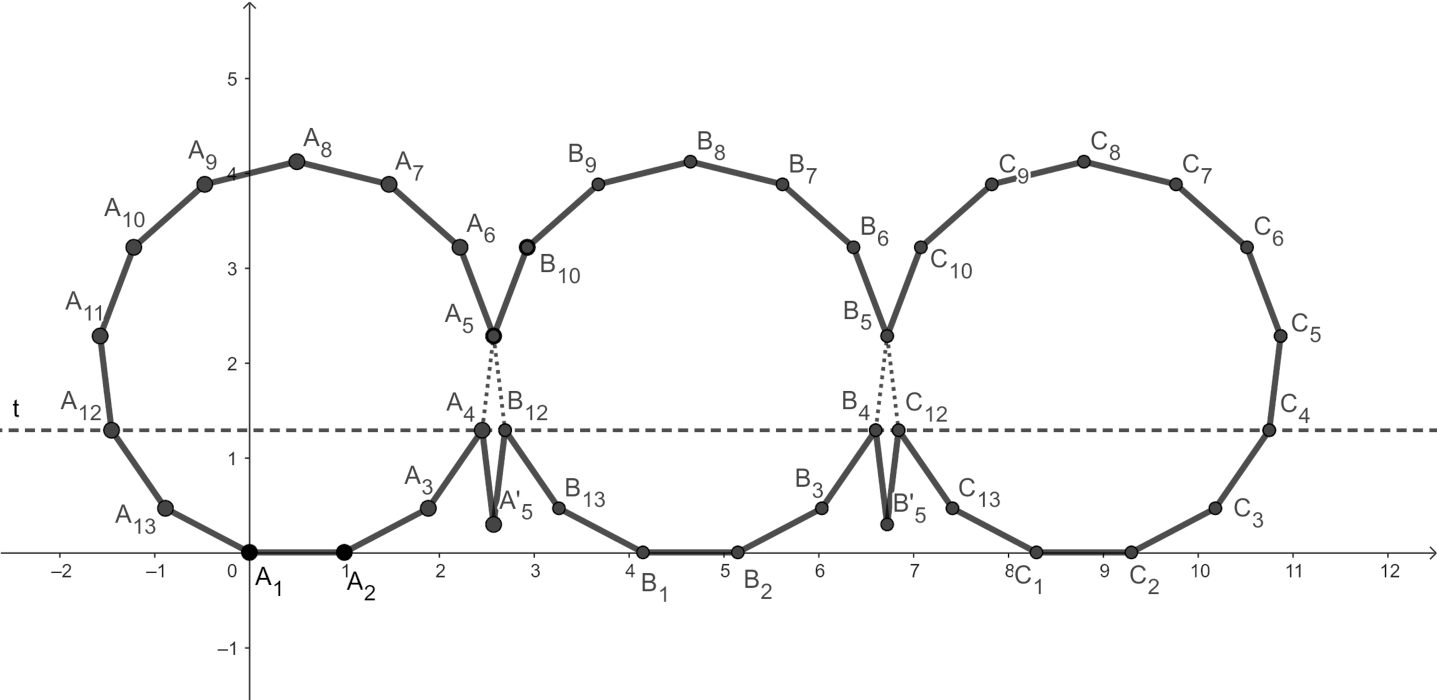
Az alábbi ábra \(\displaystyle n=39\) (azaz \(\displaystyle k=13\)) esetén mutatja be a megkonstruált sokszöget.
Ha \(\displaystyle n \geq 18\) páros és 3-mal is osztható, akkor \(\displaystyle k = n/6 \geq 3\) egész szám. Ilyenkor konstruálhatunk egy jó \(\displaystyle n\)-szöget a következő módon. Ragasszunk egy szabályos \(\displaystyle k\)-szög mindegyik oldalára 3 egybevágó fűrészfogat az alábbi módon.
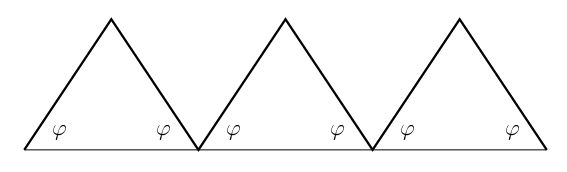
Itt minden fűrészfog egy olyan egyenlő szárú háromszög, melynek szárai egységnyi hosszúságúak, míg alapon fekvő szögei \(\displaystyle \varphi\) nagyságúak. Itt \(\displaystyle \varphi\)-t úgy kell megválasztanunk, hogy a szabályos \(\displaystyle k\)-szög különböző oldalaira állított fűrészfogak élei véletlenül se lehessenek párhuzamosak egymással. (Csak akkor állna elő ilyen elkerülendő párhuzamosság, ha \(\displaystyle 2\varphi\) a szabályos \(\displaystyle k\)-szög külső szögének, azaz \(\displaystyle \frac{360^\circ}{k}\)-nak egész számú többszöröse lenne – ez nyilván elkerülhető \(\displaystyle \varphi\) alkalmas választásával.)
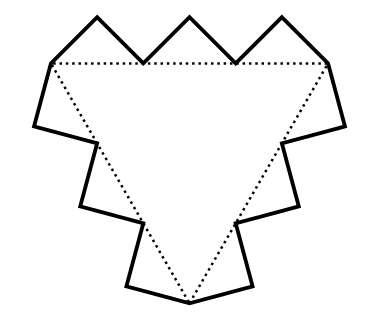
Az alábbi ábra \(\displaystyle n=18\) (azaz \(\displaystyle k=3\)) esetén mutatja be a megkonstruált sokszöget.
Statisztika:
68 dolgozat érkezett. 5 pontot kapott: Ali Richárd, Aravin Peter, Bodor Mátyás, Bogdán Balázs Ákos, Bui Thuy-Trang Nikolett, Csupor Albert Dezső, Diaconescu Tashi, Fehérvári Donát, Fórizs Emma, Gyenes Károly, Hodossy Réka, Holló Martin, Horák Zsófia, Keresztély Zsófia, Kocsis 827 Péter, Kovács Benedek Noel, Kővágó Edit Gréta, Mészáros-Komáromy Boldizsár, Sárdinecz Dóra, Szabó 721 Sámuel, Szakács Ábel, Tamás Gellért, Tömböly 299 Áron, Tran Dávid, Veres Dorottya, Vödrös Dániel László. 4 pontot kapott: Csonka Illés, Licsik Zsófia, Morvai Várkony Albert, Ozsváth Botond, Pletikoszity Martin, Prohászka Bulcsú, Virág Lénárd Dániel, Virág Tóbiás. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2023. novemberi matematika feladatai

