 |
A B. 5360. feladat (2024. január) |
B. 5360. A nem egyenlő szárú \(\displaystyle ABC\) háromszög legnagyobb szöge \(\displaystyle C\)-nél van. Jelölje a \(\displaystyle C\)-ből induló magasság talppontját \(\displaystyle T\), míg az \(\displaystyle C\)-ből induló belső szögfelező messe az \(\displaystyle AB\) oldalt az \(\displaystyle F\) pontban. Bizonyítsuk be, hogy \(\displaystyle \dfrac{AT}{TB}=\left(\dfrac{AF}{FB}\right)^2\) akkor és csak akkor teljesül, ha \(\displaystyle ACB\sphericalangle=90^\circ\).
Javasolta: Hujter Mihály (Budapest) ötlete alapján
(4 pont)
A beküldési határidő 2024. február 12-én LEJÁRT.
Megoldás. Használjuk az oldalakra az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) jelöléseket a szokásos módon, a \(\displaystyle CT\) magasságot jelölje \(\displaystyle m\), továbbá legyen \(\displaystyle AT=y\) és \(\displaystyle TB=x\). (A feltételek szerint \(\displaystyle T\) az \(\displaystyle AB\) oldal belső pontja, így \(\displaystyle x,\,y>0\); továbbá \(\displaystyle x-y\neq 0\) is teljesül.) A szögfelelezőtétel szerint \(\displaystyle AF/FB=b/a\), ezt a megoldás során többször kihasználjuk.
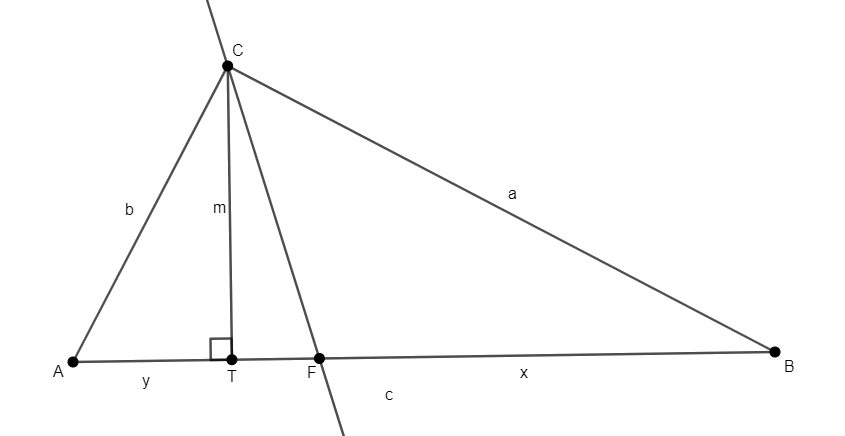
Először tegyük fel, hogy \(\displaystyle C\)-nél derékszög van. Ekkor a befogótételt felírva az \(\displaystyle a\) és \(\displaystyle b\) befogókra kapjuk, hogy \(\displaystyle cx=a^2\) és \(\displaystyle cy=b^2\). Ezekből
\(\displaystyle \frac{AT}{TB}=\frac yx=\frac{cy}{cx}=\frac{b^2}{a^2}=\left(\frac b a \right )^2=\left ( \frac {AF}{FB} \right)^2,\)
s ezzel az egyik irányt beláttuk.
Most tegyük fel, hogy \(\displaystyle AT/TB=AF^2/FB^2\). Jelöléseink, és ismét a szögfelezőtétel szerint ezt \(\displaystyle y/x=b^2/a^2\) alakban írhatjuk, amiből \(\displaystyle a^2=x/y\cdot b^2\). Használjuk a Pitagorasz-tételt az \(\displaystyle ATC\) és \(\displaystyle BTC\) háromszögekben, így \(\displaystyle b^2-y^2=m^2=a^2-x^2\). Ebből
\(\displaystyle x^2-y^2=a^2-b^2=\frac xy b^2-b^2=\frac {x-y}{y}b^2.\)
Mivel \(\displaystyle ABC\) nem egyenlő szárú, így leoszthatunk az \(\displaystyle x-y\neq 0\) kifejezéssel, amiből \(\displaystyle x+y=b^2/y\) következik. Ezt átrendezve pedig az \(\displaystyle xy=b^2-y^2=m^2\) összefüggést nyerjük. Végül ezt, és ismét a Pitagorasz-tételt az \(\displaystyle ATC\) és \(\displaystyle BTC\) háromszögekben használjuk:
\(\displaystyle c^2=(x+y)^2=x^2+y^2+2xy=a^2-m^2+b^2-m^2+2m^2=a^2+b^2.\)
A Pitagorasz-tétel megfordításából következik az állítás másik iránya, amivel a bizonyítást befejeztük.
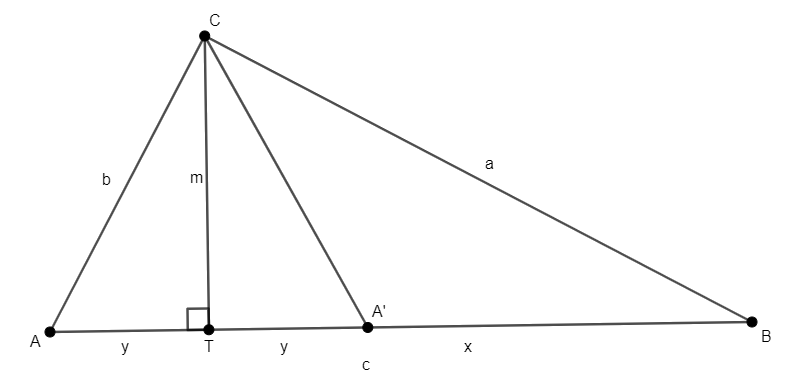
Megjegyzés: a bizonyítás második felében \(\displaystyle m^2=xy\) után lényegében a magasságtétel megfordítása történik. Ez kevéssé elterjedt állítás, hiszen ha \(\displaystyle T\) nem esik az \(\displaystyle AB\) oldalra, akkor \(\displaystyle m^2=xy\) teljesülhet nem derékszögű háromszögre is: legyen az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle a<b<c\); és tükrözzük az \(\displaystyle A\) pontot a \(\displaystyle CT\) magasságvonalra. Ekkor \(\displaystyle m\), \(\displaystyle x\) és \(\displaystyle y\) nem változik, de \(\displaystyle A'BC\) nem derékszögű. Ezért lényeges feltétel a feladatban, hogy \(\displaystyle C\)-nél van a legnagyobb szög. Érdemes továbbá megjegyezni, hogy \(\displaystyle AT/TB=AF^2/FB^2\) természetesen minden egyenlő szárú háromszögre is igaz, amelyben \(\displaystyle a=b\).
Statisztika:
A KöMaL 2024. januári matematika feladatai

