 |
A B. 5371. feladat (2024. február) |
B. 5371. Legyen \(\displaystyle P\) pont az \(\displaystyle ABC\) háromszög belső pontja. Jelölje a \(\displaystyle P\) pont merőleges vetületét a \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalakra rendre \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Bizonyítsuk be, hogy
\(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 3. \)
Javasolta: Bencze Mihály (Brassó)
(5 pont)
A beküldési határidő 2024. március 11-én LEJÁRT.
Megoldás. Legyenek a háromszög szögei \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), továbbá \(\displaystyle EAP\sphericalangle=\alpha_1\), \(\displaystyle PAF\sphericalangle=\alpha_2\), \(\displaystyle FBP\sphericalangle=\beta_1\), \(\displaystyle PBD\sphericalangle=\beta_2\) és \(\displaystyle DCP\sphericalangle=\gamma_1\), \(\displaystyle PCE\sphericalangle=\gamma_2\).
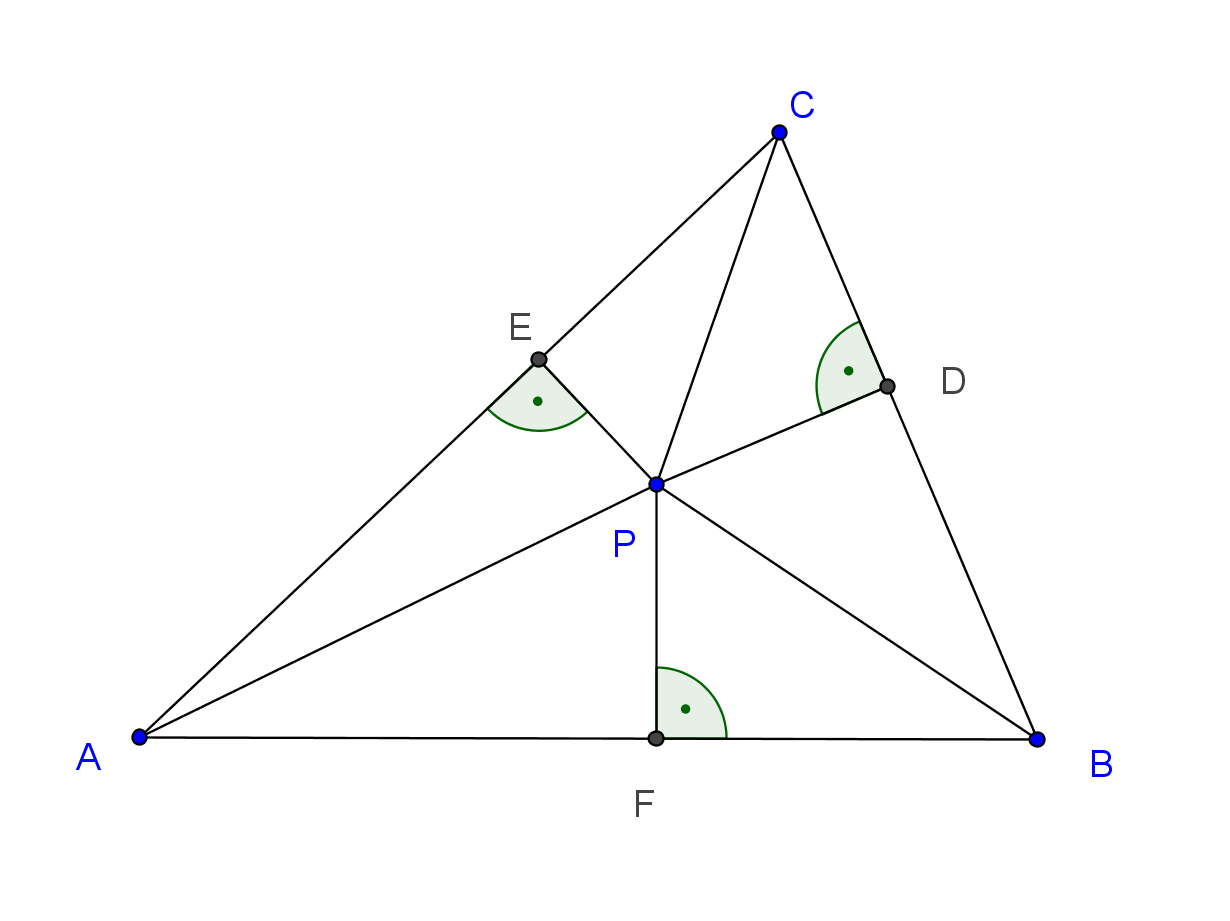
A \(\displaystyle PEA\) és \(\displaystyle PFA\) derékszögű háromszögekből a \(\displaystyle PE\) és \(\displaystyle PF\) szakaszok hosszát a \(\displaystyle PA\) szakasszal és szinusz szögfüggvénnyel is kifejezhetjük.
\(\displaystyle PE+PF=PA(\sin \alpha_1 +\sin \alpha_2). \)
A szinuszok összegére vonatkozó addíciós tétel alapján, továbbá felhasználva, hogy a koszinusz szögfüggvény értéke legfeljebb \(\displaystyle 1\), kapjuk a következő becslést:
\(\displaystyle \frac{PE+PF}{PA}=\sin \alpha_1 +\sin \alpha_2=2\sin \frac{\alpha_1+\alpha_2}{2}\cos\frac{\alpha_1-\alpha_2}{2}\le 2\sin\frac{\alpha}{2}.\)
Egyenlőség csak \(\displaystyle \alpha_1=\alpha_2\) esetén. Ugyanezzel a módszerrel kapjuk, hogy
\(\displaystyle \frac{PF+PD}{PB}\le 2\sin \frac{\beta}{2} \quad \text{és} \quad \frac{PD+PE}{PC}\le 2\sin\frac{\gamma}{2}.\)
Alkalmazzuk végül a szinuszfüggvényre és az \(\displaystyle \frac{\alpha}{2}, \frac{\beta}{2}, \frac{\gamma}{2}\) hegyesszögekre a Jensen-egyenlőtlenséget. A szinuszfüggvény a \(\displaystyle \left[0, \frac{\pi}{2} \right]\) intervallumon konkáv, ezért
\(\displaystyle \frac{PE+PF}{PA}+\frac{PF+PD}{PB}+\frac{PD+PE}{PC}\le 2\left(\sin\frac{\alpha}{2}+\sin\frac{\beta}{2}+\sin\frac{\gamma}{2}\right) \le 2\cdot 3\cdot \sin \frac{\alpha+\beta+\gamma}{6}=3.\)
Összességében egyenlőség az első becslésnél a szögfelezők esetében, míg a második becslésnél a szinuszfüggvény szigorú konkávitása miatt csak szabályos háromszög esetén teljesül. Tehát egyenlőség csak abban az esetben igaz, ha a \(\displaystyle P\) pont egy \(\displaystyle ABC\) szabályos háromszög középpontja.
Statisztika:
A KöMaL 2024. februári matematika feladatai

