A B. 5408. feladat (2024. október)

B. 5408. Egy háromszög egyik oldala számtani közepe a másik kettőnek. Bizonyítandó, hogy ezen középső oldalt kettévágó szögfelező hossza $\displaystyle \frac{\sqrt{3}}{2}$-szerese a másik két oldal mértani közepének.

Javasolta: Hujter Mihály (Budapest)

(4 pont)

A beküldési határidő 2024. november 11-én LEJÁRT.

Megoldás. Az $\displaystyle ABC$ háromszög oldalait jelölje $\displaystyle BC=a$, $\displaystyle AC=b$, $\displaystyle AB=(a+b)/2$; a $\displaystyle C$-ből induló belső szögfelező $\displaystyle CD=f$, $\displaystyle BD=k$, $\displaystyle AD=l$ az ábra szerint. A feladat feltétele: $\displaystyle k+l= \dfrac{a+b}{2}$.

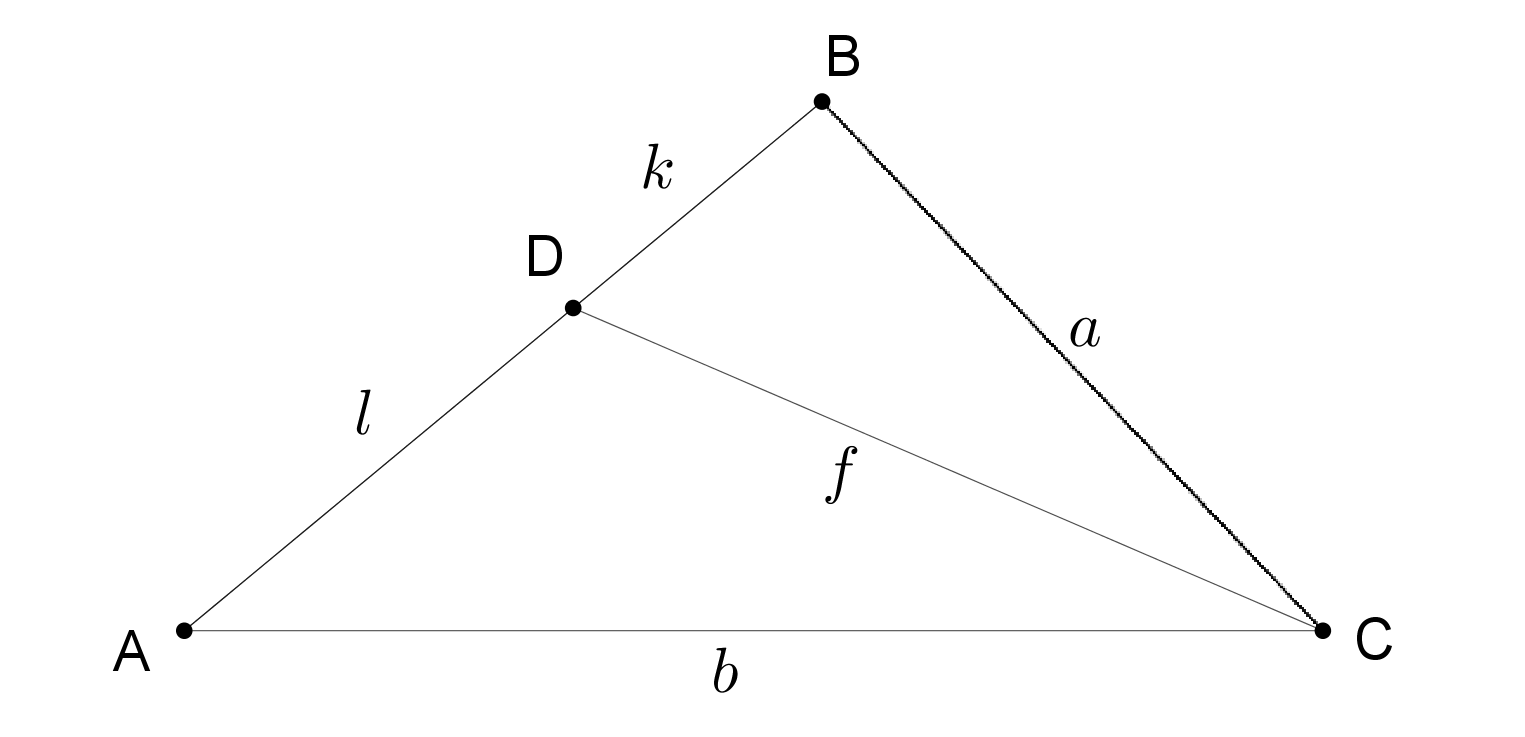
A belső szögfelezővel kapcsolatos ismert összefüggések: $\displaystyle \dfrac{k}{l} = \dfrac{a}{b}$ és $\displaystyle f^2 = ab - kl$. Az első összefüggésből $\displaystyle k=\dfrac{a}{b}\cdot l$, így

$\displaystyle \dfrac{a+b}{2} = k+l = \dfrac{a}{b}\cdot l + l = \dfrac{a+b}{b}\cdot l,$

amiből $\displaystyle l = \dfrac{b}{2}$, ezért $\displaystyle k = k+l - l = \dfrac{a+b}{2} - \dfrac{b}{2} = \dfrac{a}{2}$. Tehát valóban

$\displaystyle f^2 = ab - kl = ab - \dfrac{a}{2}\cdot \dfrac{b}{2} = \dfrac{3}{4}ab,$

azaz $\displaystyle f = \dfrac{\sqrt{3}}{2}\cdot \sqrt{ab}$.

Statisztika:

119 dolgozat érkezett.
4 pontot kapott:	55 versenyző.
3 pontot kapott:	39 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	6 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2024. októberi matematika feladatai