Problem B. 5420. (November 2024)

B. 5420. Ádám, the famous conman signed up for the following game of luck. There is a rotating table with a shape of a regular 13-gon, and at each vertex there is a black or a white cap. (Caps of the same colour are indistinguishable from each other.) Under one of the caps 1000 dollars are hidden, and there is nothing under the other caps. The host rotates the table, and then Ádám chooses a cap, and take what is underneath. Ádám's accomplice, Béla is working at the company behind this game. Béla is responsible for the placement of the 1000 dollars under the caps, however, the colors of the caps are chosen by a different collegaue. After placing the money under a cap, Béla

a) has to change the color of the cap,

b) is allowed to change the color of the cap, but he is not allowed to touch any other cap.

Can Ádám and Béla find a strategy in part a) and in part b), respectively, so that Ádám can surely find the money? (After entering the casino, Béla cannot communicate with Ádám, and he also cannot influence his colleague choosing the colors of the caps on the table.)

Proposed by Gábor Damásdi, Budapest

(6 pont)

Deadline expired on December 10, 2024.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. \(\displaystyle a)\) Ebben az esetben nem tudnak mindig működő stratégiát kitalálni.

Jelölje \(\displaystyle \mathcal{S}\) az összes lehetséges megkülönböztethető sapkakiosztás halmazát. Indirekt tegyük fel, hogy Ádám és Béla rendelkezik egy mindig működő stratégiával. Ebből a stratégiából készítsünk egy \(\displaystyle f:\mathcal{S} \to \mathcal{S}\) függvényt a következő módon: \(\displaystyle f\) egy tetszőleges \(\displaystyle s\) sapkakiosztáshoz egy olyan \(\displaystyle s'\) sapkakiosztást rendel, amely előállhat Béla sapkacseréje által. Tehát \(\displaystyle s\) az az állapot, amelyet Béla kap, és \(\displaystyle s'=f(s)\) az, amelyet Béla továbbad Ádámnak. Lehetséges, hogy a stratégia egy \(\displaystyle s\) sapkakiosztásoknál többféle cserét is megenged Bélának, ilyenkor ezek közül válasszunk ki egyet és rögzítsük ennek eredményét \(\displaystyle f(s)\) értékének.

Ahhoz, hogy Ádám mindig megtalálja a pénzt, az \(\displaystyle f\) függvénynek injektívnek kell lennie, azaz ha \(\displaystyle s \neq t\) különböző sapkakiosztások, akkor \(\displaystyle f(s) \neq f(t)\) is biztosan teljesül. Hiszen ha \(\displaystyle f(s)=f(t)\) lenne, akkor Ádám nem tudhatná biztosan, hogy \(\displaystyle s\) vagy \(\displaystyle t\) sapkakiosztásból kiindulva hozta létre Béla az \(\displaystyle f(s) = f(t)\) kiosztást. De így Ádám azt sem tudhatja biztosan, hogy hol a pénz, hiszen a pénzes sapkát képzeletben visszacserélve visszakapná azt a sapkakiosztást, amit Béla kapott a munkatársaitól (\(\displaystyle f(s)\)-ből úgy kapjuk vissza \(\displaystyle s\)-t, hogy a pénzes sapka színét megcseréljük).

Mivel \(\displaystyle \mathcal{S}\) véges halmaz, ezért ha \(\displaystyle f\) injektív, akkor szürjektívnek is kell lennie. Tehát kell legyen olyan \(\displaystyle s\) sapkakiosztás, amelyre \(\displaystyle f(s)\) a csupa fekete sapkából álló sapkakiosztás. De ha Ádám csupa fekete sapkát lát, akkor semmilyen információja nincs, amellyel a 13 egyforma sapka közül megtalálhatná a pénzt rejtőt.

\(\displaystyle b)\) Mutatunk egy biztosan működő stratégiát.

Ha Béla csupa ugyanolyan színű sapkát kap, akkor tetszőlegesen választ egyet, beteszi alá a pénzt, majd kicseréli a sapkát ellentétes színűre.

Egyéb esetekben nem cserél színt. Megnézi, hogy melyik színből van kevesebb: az általánosság korlátozása nélkül feltehetjük, hogy feketéből. Ha \(\displaystyle n\) darab fekete sapka van, akkor Béla minden fekete sapkához hozzárendel egy \(\displaystyle n\) darab pozitív egész számból álló \(\displaystyle (a_1,a_2,\ldots,a_n)\) rendezett listát (\(\displaystyle n\)-dimenziós vektort), amelynek elemei azt adják meg, hogy pozitív körüljárás szerint (az óramutatóval ellentétes irányban haladva) hány csúcsnyival kell továbbmenni a következő fekete sapkáig. Egy példa látható alább (\(\displaystyle n=5\) esetén).

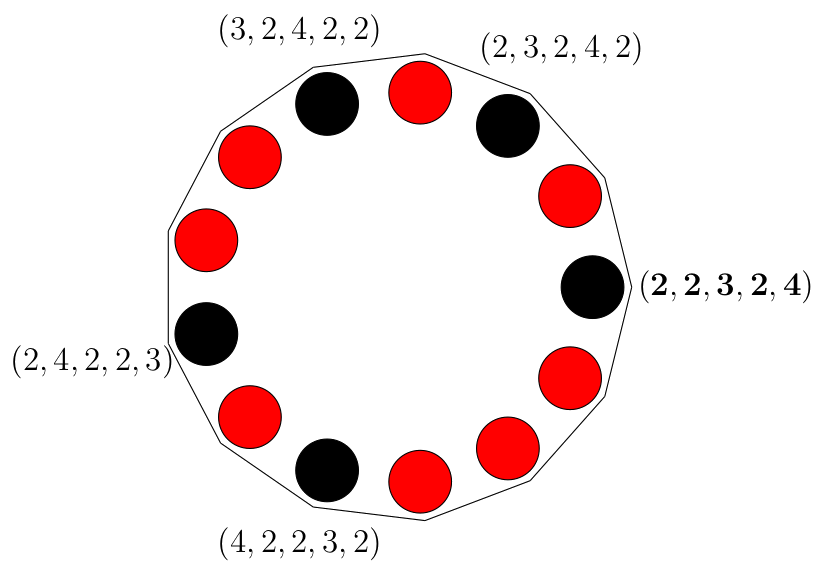
Világos, hogy mindegyik lista esetén teljesül, hogy \(\displaystyle a_1+a_2+\ldots+a_n =13\).

Lemma. Mivel a 13 prím, bármely két sapkához különböző lista fog tartozni.

A lemma bizonyítása. Indirekt feltevés: két különböző fekete sapkához írt lista, \(\displaystyle (a_1,a_2,\ldots,a_n)\) és \(\displaystyle (b_1,b_2,\ldots,b_n)\) megegyezik.

Jelölje \(\displaystyle 1 \leq t \leq n-1\), hogy az előbbi (\(\displaystyle a_i\) listás) fekete sapkától pozitív körüljárási irányba elindulva az utóbbi (\(\displaystyle b_i\) listás) fekete sapka hányadik a fekete sapkák sorában.

Világos, hogy ekkor \(\displaystyle b_1=a_{1+t},b_2 = a_{2+t}\) és általában \(\displaystyle b_i = a_{i+t}\), ha az indexeket modulo \(\displaystyle n\) tekintjük. Mivel az \(\displaystyle a_i\) és a \(\displaystyle b_i\) sorozat megegyezik, ezért \(\displaystyle a_i = a_{i+t} = a_{i+2t} = \ldots = a_{i+kt}\) minden \(\displaystyle k\) pozitív egészre. Az

\(\displaystyle i, i+t, i+2t, \ldots, i+kt, \ldots \)

indexsorozat két tagja, \(\displaystyle i+k_1t\) és \(\displaystyle i+k_2t\) akkor egyezik meg modulo \(\displaystyle n\), ha \(\displaystyle n \mid (k_2-k_1) t\), azaz \(\displaystyle \frac{n}{(n,t)} \mid k_2-k_1\). Következésképpen

\(\displaystyle i, i+t, \ldots, i+\frac{n}{(n,t)}t \)

modulo \(\displaystyle n\) nézve is csupa különböző index, míg \(\displaystyle k > \frac{n}{(n,t)}\) esetén \(\displaystyle i+kt\) megegyezik valamelyik felsorolt indexszel (mod \(\displaystyle n\)).

Ezzel az \(\displaystyle \{ 1,2,\ldots,n \}\) indexhalmazt felosztottuk \(\displaystyle (n,t)\) darab \(\displaystyle \frac{n}{(n,t)}\) tagú csoporta úgy, hogy ha az \(\displaystyle i\) és \(\displaystyle j\) indexek ugyanazon csoportba tartoznak, akkor valamilyen \(\displaystyle k\)-ra \(\displaystyle i + kt \equiv j\) (mod \(\displaystyle n\)), amiből persze következik, hogy \(\displaystyle a_i = a_j\).

(Az ekvivalencia-reláció fogalmát használva így fogalmazhatunk: Az \(\displaystyle \{1,2,\ldots,n\}\) halmazon a \(\displaystyle t\) konstans definiálja a \(\displaystyle i \sim j\) relációt, amely akkor teljesül, ha valamilyen \(\displaystyle k\)-ra \(\displaystyle i + kt \equiv j\) mod \(\displaystyle n\). Világos, hogy \(\displaystyle \sim\) ekvivalencia-reláció. Fentebb lényegében azt láttuk be, hogy a \(\displaystyle \sim\) reláció \(\displaystyle (n,t)\) darab, egyenként \(\displaystyle \frac{n}{(n,t)}\) elemű ekvivalencia-osztályra bontja az alaphalmazt.)

De ezek szerint az \(\displaystyle a_1,a_2,\ldots,a_n\) sorozatban minden szám \(\displaystyle \frac{n}{(n,t)} \ell\)-szer szerepel (valamilyen \(\displaystyle 1 \leq \ell \leq (n,t)\) egészre). Ebből az következik, hogy

\(\displaystyle \frac{n}{(n,t)} \mid a_1 + a_2 + \ldots + a_n = 13. \)

Ez viszont lehetetlen, mivel \(\displaystyle 1 < \frac{n}{(n,t)} \leq 6\), míg 13 prímszám. (\(\displaystyle 1 < \frac{n}{(n,t)}\) abból következik, hogy \(\displaystyle t \leq n-1\), másrészt pedig \(\displaystyle \frac{n}{(n,t)} \leq n \leq 6\).) Ezzel a lemmát beláttuk.

Tudjuk tehát, hogy mindegyik fekete sapkához különböző lista tartozik. Béla ezek közül a listák közül kiválasztja a lexikografikusan legelsőt (pl. a fenti ábrán a \(\displaystyle (2,2,3,2,4)\) lesz ez) és elrejti alá a pénzt; a sapkát nem cseréli ki. Ugyanezeket a listákat Ádám is le tudja gyártani, megkeresi a lexikografikusan legelsőt, és kiveszi alóla a pénzt. Ha Ádám csak egyetlen fekete (vagy egyetlen piros) sapkát lát, akkor persze nem fogja tudni, hogy ez a sapka cserélve lett-e vagy sem. De a pénzt biztosan megtalálja alatta.

Statistics:

41 students sent a solution.
6 points:	Ali Richárd, Baran Júlia, Bencze Mátyás, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Görömbey Tamás, Hodossy Réka, Holló Martin, Kovács Benedek Noel, Molnár István Ádám, Pázmándi József Áron, Péter Hanna, Pletikoszity Martin, Rajtik Sándor Barnabás, Sárdinecz Dóra, Sütő Áron, Szabó 721 Sámuel, Tamás Gellért, Virág Tóbiás, Vödrös Dániel László, Wágner Márton.
4 points:	8 students.
3 points:	2 students.
2 points:	1 student.
1 point:	2 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, November 2024