A B. 5431. feladat (2025. január)

B. 5431. Az \(\displaystyle ABC\) háromszög beírt köre \(\displaystyle k\), a \(\displaystyle k\) középpontja \(\displaystyle I\). Az \(\displaystyle AI\) egyenes \(\displaystyle k\)-t \(\displaystyle A\)-hoz közelebb \(\displaystyle D\)-ben, \(\displaystyle A\)-tól távolabb \(\displaystyle E\)-ben metszi. Legyen \(\displaystyle k\) érintési pontja \(\displaystyle AC\)-n \(\displaystyle F\). Az \(\displaystyle E\) pontban a \(\displaystyle k\)-hoz húzott érintő \(\displaystyle AC\)-t \(\displaystyle G\)-ben metszi. Igazoljuk, hogy \(\displaystyle GI\) párhuzamos \(\displaystyle FD\)-vel.

Javasolta: Lovas Márton (Budakalász)

(3 pont)

A beküldési határidő 2025. február 10-én LEJÁRT.

Megoldás.

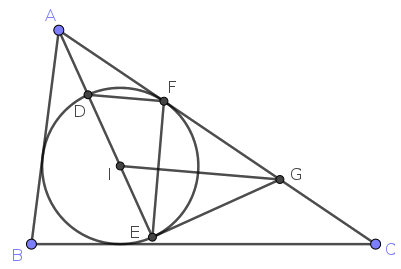
Egyrészt a beírt körnek \(\displaystyle DE\) átmérője, ezért a Thalész-tétel szerint \(\displaystyle EFD \sphericalangle = 90^{\circ}\), azaz \(\displaystyle DF \perp EF\).

Másrészt \(\displaystyle E\) és \(\displaystyle F\), mint a \(\displaystyle G\)-ből a beírt körhöz húzott érintők érintési pontjai a \(\displaystyle GI\) tengelyre nézve egymás tükörképei, tehát \(\displaystyle GI \perp EF\).

Ezzel beláttuk, hogy \(\displaystyle DF\) és \(\displaystyle GI\) is merőleges az \(\displaystyle EF\) egyenesre, tehát egymással párhuzamosak.

Statisztika:

83 dolgozat érkezett.
3 pontot kapott:	69 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. januári matematika feladatai