A B. 5433. feladat (2025. január)

B. 5433. Mutassuk meg, hogy tetszőleges négyszög alapú gúlában az oldallapok súlypontjait a szemközti alapél felezőpontjával összekötő szakaszok egy ponton mennek át.

Javasolta: Kiss Géza (Csömör)

(4 pont)

A beküldési határidő 2025. február 10-én LEJÁRT.

Megoldás. Legyen a gúla alaplapja az \(\displaystyle ABCD\) négyszög, csúcsa az \(\displaystyle E\) pont. Az \(\displaystyle AB\) él felezőpontja \(\displaystyle F\), a \(\displaystyle CD\) él felezőpontja pedig \(\displaystyle H\). Az \(\displaystyle ABE\) oldallap \(\displaystyle G\) súlypontja az \(\displaystyle EF\) szakasz \(\displaystyle F\)-hez közelebbi harmadolópontja, míg a \(\displaystyle CDE\) lap \(\displaystyle J\) súlypontja az \(\displaystyle EH\) szakasz \(\displaystyle H\)-hoz közelebbi harmadolópontja. Tehát az \(\displaystyle E\), \(\displaystyle G\), \(\displaystyle F\), \(\displaystyle H\), \(\displaystyle J\) pontok mind egy síkban vannak. Rajzoljuk le ezt a síkmetszetet!

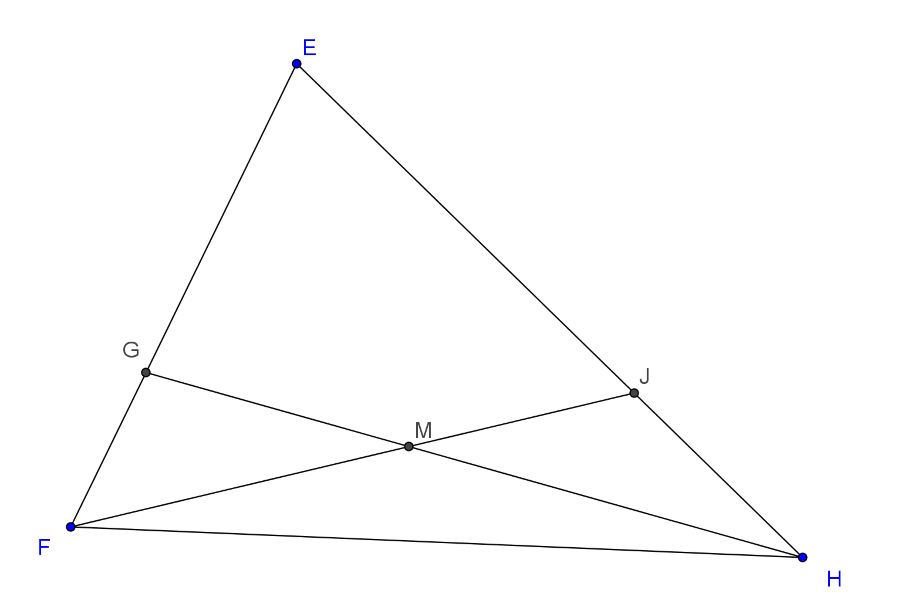
A feladatban is szereplő két szakasz \(\displaystyle GH\) és \(\displaystyle FJ\). Ezek metszéspontja legyen \(\displaystyle M\) pont. Az \(\displaystyle M\) pont helyzetének meghatározásához a vektorokat hívjuk segítségül. Legyen \(\displaystyle \overrightarrow{EF}=\mathbf x, ~\overrightarrow{EH}=\mathbf y\), ennek megfelelően \(\displaystyle \overrightarrow{EG}=\frac23 \mathbf x, ~\overrightarrow{EJ}=\frac23 \mathbf y\).

Az \(\displaystyle M\) pont az \(\displaystyle FJ\) egyenes pontja, ezért az \(\displaystyle \overrightarrow{EM}\) vektor felírható az \(\displaystyle \overrightarrow{EF}\) és \(\displaystyle \overrightarrow{EJ}\) vektorok lineáris kombinációjaként úgy, hogy a két számszorzó összege 1. (Lásd még az előző számban a B5427. feladat megoldása során felhasznált első állítást.) Nevezetesen:

\(\displaystyle \overrightarrow{EM}=\lambda \mathbf x+(1-\lambda)\frac23 \mathbf y.\)

Az \(\displaystyle M\) pont a \(\displaystyle GH\) egyenesnek is pontja ezért megfelelő \(\displaystyle \mu\) és \(\displaystyle (1-\mu)\) szorzókkal:

\(\displaystyle \overrightarrow{EM}=\mu \frac23\mathbf x+(1-\mu)\mathbf y.\)

Az \(\displaystyle EFH\) sík minden vektora egyértelműen írható fel az \(\displaystyle \mathbf x\) és \(\displaystyle \mathbf y\) vektorok lineáris kombinációjaként, ezért a kétféle felírásnak meg kell egyeznie:

\(\displaystyle \overrightarrow{EM}=\lambda \mathbf x+(1-\lambda)\frac23 \mathbf y=\mu \frac23\mathbf x+(1-\mu)\mathbf y,\)

\(\displaystyle \lambda=\frac{2}{3}\mu \quad \text{és} \quad \frac{2}{3}(1-\lambda)=1-\mu.\)

\(\displaystyle \lambda\) kifejezett értékét a második egyenletbe helyettesítve \(\displaystyle \mu=\frac35\) és \(\displaystyle \lambda=\frac25\) adódik, vagyis az \(\displaystyle M\) pont \(\displaystyle 2:3\) arányban osztja ketté a \(\displaystyle GH\) szakaszt.

Most irányítsunk a tér egy tetszőleges \(\displaystyle O\) pontjából a gúla csúcsaiba vektorokat. Legyenek ezek a csúcsoknak megfelelően \(\displaystyle \mathbf a, ~\mathbf b, ~\mathbf c, ~\mathbf d\) és \(\displaystyle \mathbf e\) vektorok. Az \(\displaystyle \overrightarrow{OG}=\frac{\mathbf a+\mathbf b+\mathbf e}{3}\), mert az \(\displaystyle ABE\) súlypontjába mutat, továbbá \(\displaystyle \overrightarrow{OH}=\frac{\mathbf c+\mathbf d}{2}\), mivel \(\displaystyle H\) a \(\displaystyle CD\) él felezőpontja. Végül az \(\displaystyle M\) pont \(\displaystyle 2:3\) arányban osztja a \(\displaystyle GH\) szakaszt, így az osztópontokra ismert formula alapján:

\(\displaystyle \overrightarrow{OM}=\frac{3}{5}\frac{\mathbf a+\mathbf b+\mathbf e}{3}+\frac{2}{5}\frac{\mathbf c+\mathbf d}{2}=\frac{\mathbf a+\mathbf b+\mathbf c+\mathbf d+\mathbf e}{5}.\)

Látjuk, hogy az \(\displaystyle M\) pont éppen a gúla súlypontja. Az összes többi oldallapok súlypontját összekötve a szemközti alapél felezőpontjával teljesen analóg módon kapjuk, hogy mindegyik szakasz átmegy a gúla súlypontján.

Megjegyzés: Ismerve az eredményt már azt is látjuk, hogy nincsen arra szükség, hogy a pontok egy gúla csúcsai legyenek. Bármely öt pontra a térben igaz lesz, hogy három pont által meghatározott hármas súlypontját összekötve a maradék kettő felezőpontjával a pontrendszer súlypontján átmenő szakaszokat kapunk.

Statisztika:

68 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Aravin Peter, Beinschroth Máté, Bodor Ádám, Bolla Donát Andor, Bővíz Dániel, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Diaconescu Tashi, Fodor Barna, Guthy Gábor, Gyenes Károly, Hajba Milán, Hajszter Dóra, Harkay Ákos, Hideg János, Hodossy Réka, Holló Martin, Járdánházi-Kurutz Vilmos, Kerekes András, Kovács Benedek Noel, Kővágó Edit Gréta, Li Mingdao, Maróti Bálint, Mikó Hédi Irma, Molnár István Ádám, Molnár Lili, Nagy 707 Botond, Nagypál Katóca, Pázmándi József Áron, Péter Hanna, Prohászka Bulcsú, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Sárdinecz Dóra, Sha Jingyuan, Sun Wen Ze, Sütő Áron, Szabó 721 Sámuel, Tamás Gellért, Török Eszter Júlia, Vámosi Bendegúz Péter, Varga 511 Vivien, Vigh 279 Zalán, Virág Lénárd Dániel, Vödrös Dániel László, Wágner Márton, Zhai Yu Fan.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2025. januári matematika feladatai