A B. 5437. feladat (2025. január)

B. 5437. Az \(\displaystyle ABC\) háromszögben \(\displaystyle BC<AC\), és \(\displaystyle D\) olyan pont az \(\displaystyle AC\) oldalon, hogy \(\displaystyle BC=DC\). A \(\displaystyle \Gamma\) kör belülről érinti az \(\displaystyle ABC\) háromszög köréírt körének \(\displaystyle B\)-t nem tartalmazó \(\displaystyle AC\) ívét \(\displaystyle X\)-ben, valamint érinti \(\displaystyle AC\)-t \(\displaystyle D\)-ben. A \(\displaystyle B\)-ből \(\displaystyle \Gamma\)-hoz húzott \(\displaystyle C\)-hez közelebbi érintő \(\displaystyle AC\)-t \(\displaystyle Y\)-ban metszi, \(\displaystyle \Gamma\)-t pedig \(\displaystyle Z\)-ben érinti. Igazoljuk, hogy ha \(\displaystyle A\), \(\displaystyle Y\), \(\displaystyle X\), és az \(\displaystyle ABC\) háromszög körülírt körének középpontja egy körön helyezkednek el, akkor \(\displaystyle AZ=CZ\).

Javasolta: Lovas Márton (Budakalász)

(6 pont)

A beküldési határidő 2025. február 10-én LEJÁRT.

Megoldás. Először megmutatjuk, hogy \(\displaystyle Z\) a \(\displaystyle CX\) szakasz belsejébe esik, és \(\displaystyle AYZX\) húrnégyszög. Ehhez nem lesz szükségünk az \(\displaystyle O\) helyzetére.

Tekintsük a \(\displaystyle C\) középpontú, a \(\displaystyle B,D\) pontokon átmenő körre való inverziót. A különböző objektumokat vesszővel fogjuk jelölni. Világos, hogy \(\displaystyle B'=B\), \(\displaystyle D'=D\), \(\displaystyle (CA)'=CA\) és \(\displaystyle (CX)'=CX\). Mivel \(\displaystyle CD\) a \(\displaystyle D\) pontban érinti \(\displaystyle \Gamma\)-t, \(\displaystyle \Gamma'=\Gamma\).

Az \(\displaystyle X'\) pont a \(\displaystyle \Gamma\) kör és a \(\displaystyle CX\) egyenes második, \(\displaystyle X\)-től különböző metszéspontja. Az \(\displaystyle ABCX\) kör átmegy az inverzió pólusán, ezért \(\displaystyle (ABCX)'=BX'\). Mivel az \(\displaystyle ABCX\) kör \(\displaystyle X\)-ben érinti \(\displaystyle \Gamma\)-t, a képeik, a \(\displaystyle BX'\) egyenes és \(\displaystyle \Gamma\) is érintik egymást az \(\displaystyle X'\) pontban.

A \(\displaystyle CX\) szakasz a körülírt kör húrja, ezért mindenképpen elmetszi a \(\displaystyle \Gamma\) kört. Ezért \(\displaystyle BX'\) a \(\displaystyle B\)-ből \(\displaystyle \Gamma\)-hoz húzott, \(\displaystyle C\)-hez közelebbi éríntő, vagyis \(\displaystyle X'=Z\).

Végül, \(\displaystyle Y=BZ\cap AC=(ABCX)'\cap(AC)'=A'\). Az inverzió tulajdonságai miatt az \(\displaystyle A\), \(\displaystyle X\), \(\displaystyle A'=Y\) és \(\displaystyle X'=Z\) pontok egy körön vagy egyenesen vannak, de egyenesre nem eshetnek, mert akkor ez az egyenes tartalmazná az \(\displaystyle A,C,X\) pontokat.

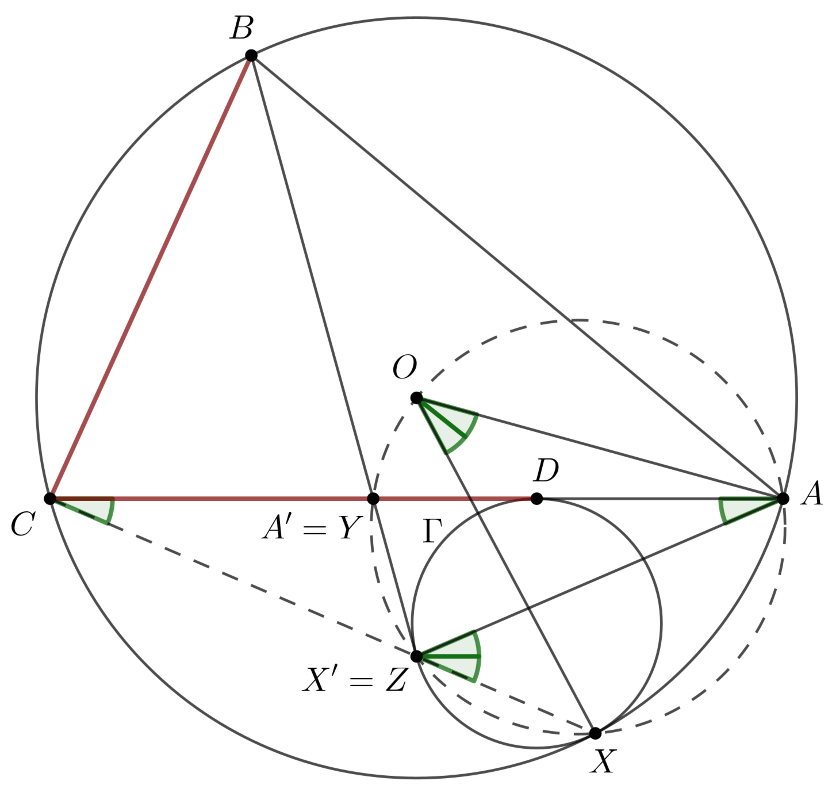
Ezek után, a fentiek és feladat feltételei szerint \(\displaystyle Z\) és \(\displaystyle O\) is az \(\displaystyle AXY\) körön van. Az \(\displaystyle ACZ\) háromszög szögeiből, valamint a kerületi és középponti szögek tételéből

\(\displaystyle ACZ\sphericalangle+ZAC\sphericalangle = AZX\sphericalangle = AOX\sphericalangle = 2ACX\sphericalangle = 2ACZ\sphericalangle, \)

tehát \(\displaystyle ZAC\sphericalangle=ACZ\sphericalangle\), az \(\displaystyle ACZ\) háromszög egyenlő szárú, és \(\displaystyle AZ=CZ\).

Statisztika:

16 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Holló Martin, Kovács Benedek Noel, Minh Hoang Tran, Prohászka Bulcsú, Sárdinecz Dóra, Sha Jingyuan, Vigh 279 Zalán, Virág Tóbiás.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2025. januári matematika feladatai