A B. 5472. feladat (2025. szeptember)

B. 5472. Az \(\displaystyle ABCD\) konvex négyszögben \(\displaystyle AB=BC=CD\). Igazoljuk, hogy ha \(\displaystyle BCD\sphericalangle=2DAB\sphericalangle\), akkor \(\displaystyle ABC\sphericalangle=2CDA\sphericalangle\).

Javasolta: Kós Géza (Budapest) és Vígh Viktor (Sándorfalva)

(4 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Megoldás. Legyen a négyszög \(\displaystyle A\) csúcsnál fekvő szöge \(\displaystyle \alpha\), a \(\displaystyle D\) csúcsnál fekvő szöge \(\displaystyle \delta\). A feladat feltétele alapján \(\displaystyle BCD\sphericalangle=2\alpha\) és bizonyítanunk kell, hogy \(\displaystyle ABC\sphericalangle=2\delta\).

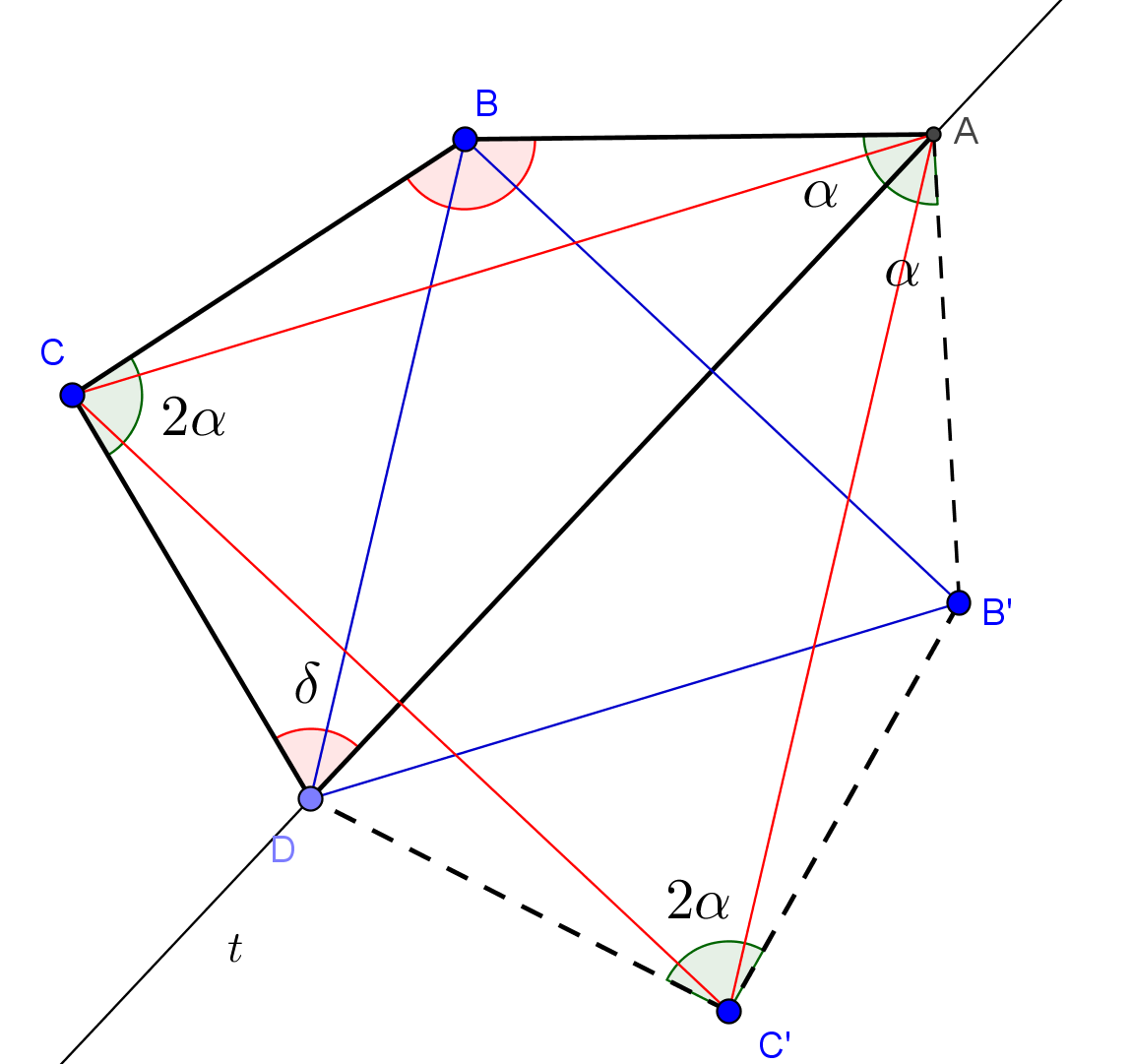
Tükrözzük a négyszöget az \(\displaystyle AD\) oldalegyenesre. \(\displaystyle B\) és \(\displaystyle C\) pontok tükörképei az ábra szerint rendre \(\displaystyle B'\) és \(\displaystyle C'\). Így kapjuk az \(\displaystyle ABCDC'B'\) hatszöget. A tükrözés és a feltétel miatt egyrészt

\(\displaystyle B'AB\sphericalangle=BCD\sphericalangle=DC'B'\sphericalangle=2\alpha,\)

másrészt a hatszögnek mindegyik oldala ugyanakkora, így a \(\displaystyle B'AB, ~BCD\) és \(\displaystyle DC'B'\) háromszögek egybevágók, a \(\displaystyle BDB'\) háromszög szabályos.

Így \(\displaystyle ABC,~CDC'\) és \(\displaystyle C'B'A\) egybevágó egyenlő szárú háromszögek, hiszen két-két száruk a négyszög egyenlő oldalai vagy azok tükörképei közül kerül ki, szárszögeik pedig a \(\displaystyle B'AB, ~BCD\) és \(\displaystyle DC'B'\) háromszögek egybevágósága alapján s azt felhasználva, hogy a \(\displaystyle BDB'\) háromszög oldalaira kifelé írtak ugyanakkorák. Így \(\displaystyle ABC \sphericalangle = CDC' \sphericalangle = 2 \cdot CDA \sphericalangle = 2 \delta\), éppen ezt szerettük volna bizonyítani.

Diszkusszió. A \(\displaystyle CDC' \sphericalangle = 2 \cdot CDA \sphericalangle\) egyenlőségnél kihasználjuk, hogy \(\displaystyle CDA\sphericalangle = \delta\) hegyesszög (azaz \(\displaystyle D\) és \(\displaystyle A\) a \(\displaystyle CC'\) egyenes különböző oldalára esik). Ez következik a feladat feltételeiből, mint azt a következőkben belátjuk.

Az \(\displaystyle ABCD\) négyszög konvex, így \(\displaystyle \alpha\) biztosan hegyesszög. Az \(\displaystyle ABC\) szögről tudjuk, hogy konvex, továbbá

\(\displaystyle ABC\sphericalangle=ABB'\sphericalangle+60^\circ+DBC\sphericalangle=60^\circ+2(90^\circ-\alpha)<180^\circ. \)

Innen rendezéssel \(\displaystyle \alpha>30^\circ\), és így:

\(\displaystyle \delta = ADB\sphericalangle + BDC\sphericalangle = 30^\circ + (90^\circ-\alpha) < 90^\circ. \)

Statisztika:

105 dolgozat érkezett.
4 pontot kapott:	71 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2025. szeptemberi matematika feladatai