A B. 5475. feladat (2025. szeptember)

B. 5475. Mutassunk példát olyan szabályos sokszögre, amelynek a területe egyenlő valamelyik két átlójának szorzatával.

Javasolta: Hujter Mihály (Budapest)

(4 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Megoldás. Van ilyen szabályos sokszög. Legyen \(\displaystyle A_1A_2A_3A_4\ldots A_{11}A_{12}\) egy szabályos 12-szög, jelölje a körülírt körének sugarát \(\displaystyle r\), középpontját \(\displaystyle K\).

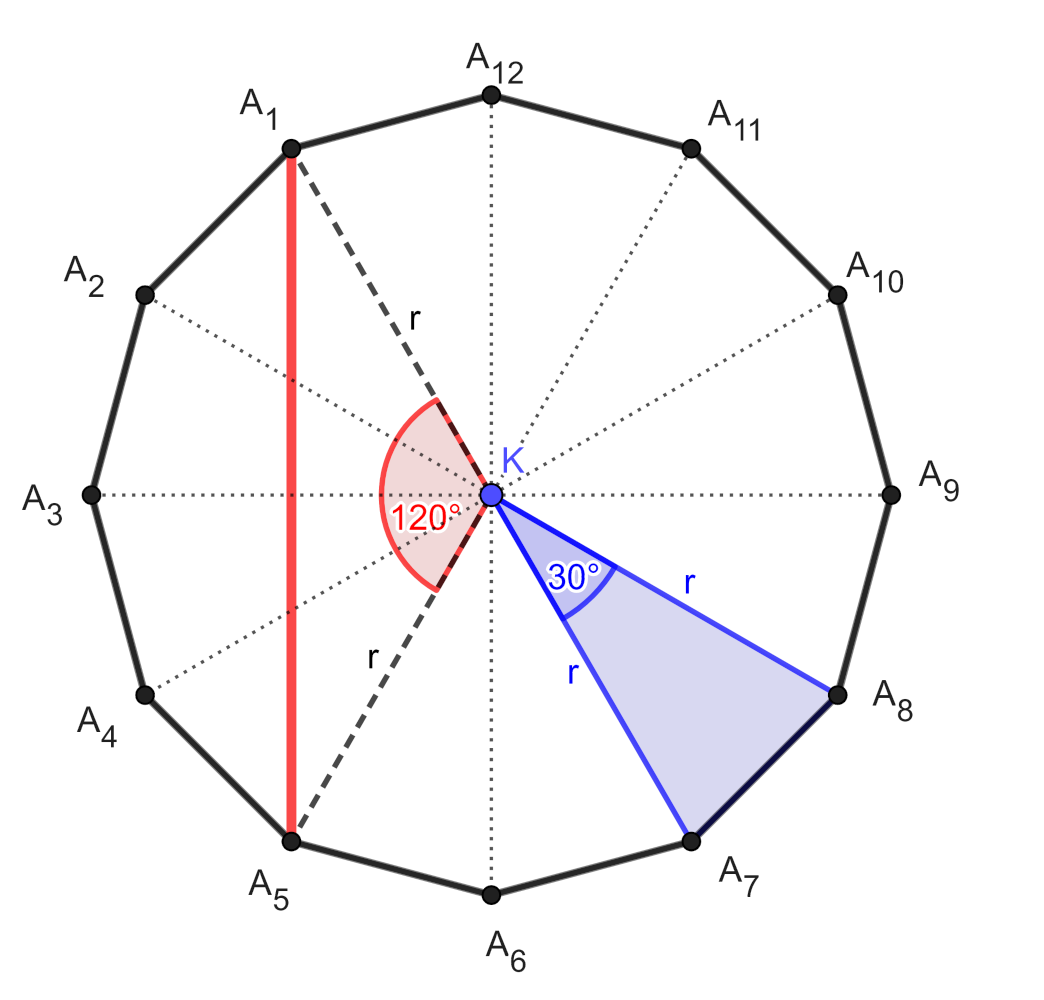
A csúcsokat a középponttal összekötve a sokszöget 12 olyan egybevágó egyenlő szárú háromszögre vágjuk, melyek szárainak hossza \(\displaystyle r\), a szárak által bezárt szög pedig \(\displaystyle \frac{360^\circ}{12}\). Egy ilyen háromszög területe \(\displaystyle \frac{r^2 \sin(30^\circ)}{2} = \frac{r^2}{4}\), tehát a 12-szög területe ennek 12-szerese, azaz \(\displaystyle 3r^2\).

\(\displaystyle KA_1A_5\) egy olyan egyenlő szárú háromszög, amelynek \(\displaystyle KA_1\) és \(\displaystyle KA_5\) szárai \(\displaystyle 4 \cdot 30^\circ = 120^\circ\)-os szöget zárnak be, tehát \(\displaystyle A_1A_5 = \sqrt{3} r\). (Ez kiszámítható pl. koszinusztétellel, vagy fél szabályos háromszögekre hivatkozva).

Található másik ugyanilyen hosszú átló (pl. \(\displaystyle A_2A_6\)) is a 12-szögben, ezek hosszának szorzata éppen \(\displaystyle 3r^2\).

Statisztika:

117 dolgozat érkezett.
4 pontot kapott:	82 versenyző.
3 pontot kapott:	13 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. szeptemberi matematika feladatai