A B. 5477. feladat (2025. szeptember)

B. 5477. Az \(\displaystyle ABCD\) húrnégyszög köré írt kör \(\displaystyle \Omega\). Az \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök belülről érintik \(\displaystyle \Omega\)-t, és mindkettő érinti az \(\displaystyle AB\) és a \(\displaystyle CD\) szakaszt is. Az \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) a \(\displaystyle P\) és \(\displaystyle Q\) pontokban metszik egymást. Mutassuk meg, hogy a \(\displaystyle PQ\) egyenes felezi az \(\displaystyle \Omega\) kör \(\displaystyle AB\) és \(\displaystyle CD\) íveit.

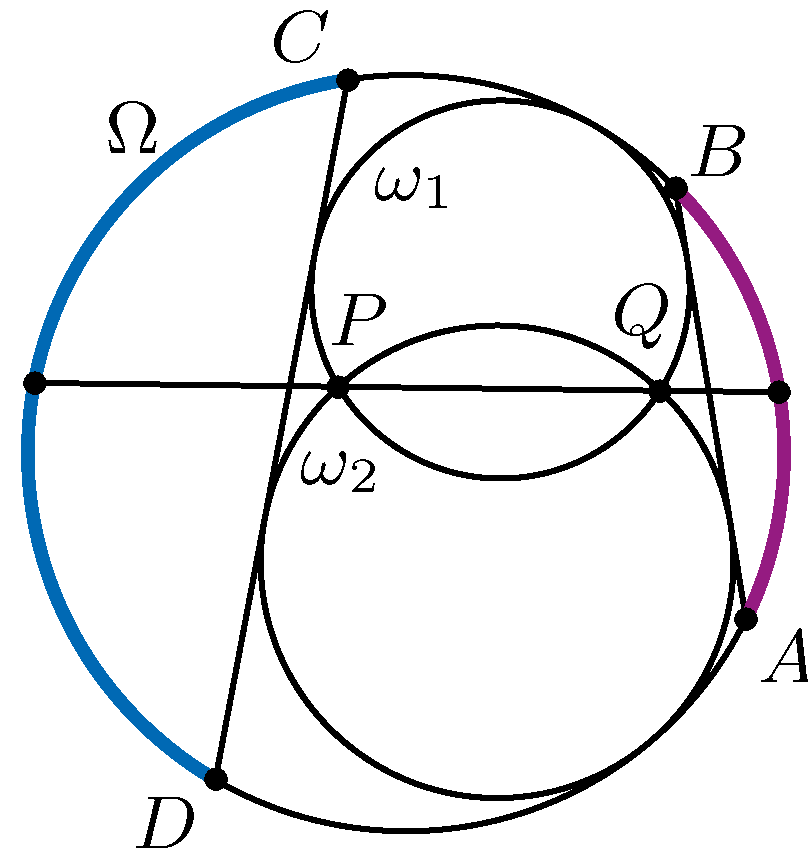
Javasolta: Kós Géza (Budapest)

(6 pont)

A beküldési határidő 2025. október 10-én LEJÁRT.

Megoldás. Legyen \(\displaystyle M\) a \(\displaystyle CD\) ív felezőpontja, és \(\displaystyle T,U,V,W\) az ábrán megjelölt érintési pontok.

Az \(\displaystyle \Omega\)-hoz \(\displaystyle M\)-ben húzott érintő párhuzamos \(\displaystyle CD\)-vel, ami éppen az \(\displaystyle \omega_1\)-hez \(\displaystyle V\)-ben húzott érintő. Mivel \(\displaystyle T\) az \(\displaystyle \omega_1\) és \(\displaystyle \Omega\) külső (pozitív arányú) hasonlósági pontja, az érintők párhuzamossága miatt az \(\displaystyle \omega_1\)-t \(\displaystyle \Omega\)-ba vivő, \(\displaystyle T\) középpontú centrális hasonlóság \(\displaystyle V\)-t \(\displaystyle M\)-be képezi, ezért \(\displaystyle T\), \(\displaystyle V\) és \(\displaystyle M\) kollineárisak. Ugyanígy \(\displaystyle U\), \(\displaystyle W\) és \(\displaystyle M\) is kollineárisak.

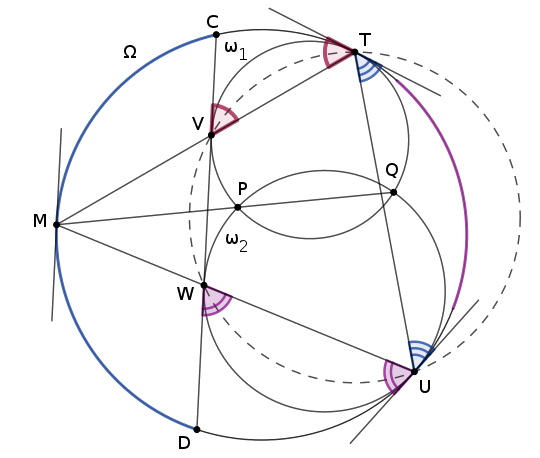
Vegyük észre, hogy \(\displaystyle \omega_1\) körben a \(\displaystyle V\) és \(\displaystyle T\) pontokban húzott érintők egyenlő szögeket zárnak be a \(\displaystyle VT\) húrral, ezért az ábrán egy vonallal jelölt szögek egyenlőek. Ugyanígy indokolhatunk \(\displaystyle \omega_2\) kör és \(\displaystyle WU\) húr esetén, így kapjuk a kétvonalas szögek egyenlőségét; valamint \(\displaystyle \Omega\) kör és \(\displaystyle TU\) húr esetén, amiből a háromvonalas szögek egyenlősége következik. A \(\displaystyle TVWU\) négyszögben a \(\displaystyle W\) és \(\displaystyle T\) szögek kiegészítő szögeinek összege éppen egy egyvonalas, egy kétvonalas és egy háromvonalas szög. Ugyanígy a \(\displaystyle V\) és \(\displaystyle U\) szögek kiegészítő szögeinek összege éppen egy egyvonalas, egy kétvonalas és egy háromvonalas szög. Ebből következik, hogy \(\displaystyle W\sphericalangle+T\sphericalangle=V\sphericalangle+U\sphericalangle\), s így \(\displaystyle TVWU\) húrnégyszög.

A \(\displaystyle TVWU\) kör és \(\displaystyle \omega_1\) hatványvonala \(\displaystyle TV\), míg \(\displaystyle TVWU\) kör és \(\displaystyle \omega_2\) hatványvonala \(\displaystyle UW\), ezért \(\displaystyle M=TV\cap UW\) az \(\displaystyle \omega_1\), \(\displaystyle \omega_2\) és \(\displaystyle TVWU\) körök hatványpontja. A \(\displaystyle CD\) ívet felező \(\displaystyle M\) hatványpont pedig illeszkedik \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\) körök \(\displaystyle PQ\) hatványvonalára, azaz \(\displaystyle PQ\) valóban felezi a \(\displaystyle CD\) ívet. Ugyanígy igazolható, hogy \(\displaystyle PQ\) az \(\displaystyle AB\) ívet is felezi. Ezzel az állítást beláttuk.

Megjegyzés. Közismert, hogy ha adott négy kör, \(\displaystyle k_1,k_2,k_3,k_4\), és minden \(\displaystyle i\)-re \(\displaystyle k_i\) és \(\displaystyle k_{i+1}\) kívülről érintik egymást (\(\displaystyle k_5\equiv k_1\)); akkor a négy érintési pont egy körön van. Ennek egy változatát használtuk a megoldásban, ahol \(\displaystyle VW\) egyenes játssza az egyik kör szerepét, és az érintések sem mind külsők.

Statisztika:

27 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Bodor Ádám, Diaconescu Tashi, Ercse Ferenc, Gyenes Károly, Hideg János, Holló Martin, Horák Zsófia, Kerekes András, Li Mingdao, Pázmándi József Áron, Rajtik Sándor Barnabás, Sánta Gergely Péter, Sha Jingyuan, Wágner Márton, Zhai Yu Fan.
5 pontot kapott:	Sajter Klaus, Varga 511 Vivien, Vincze Marcell.
4 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2025. szeptemberi matematika feladatai