A B. 5486. feladat (2025. november)

B. 5486. Az \(\displaystyle ABCD\) konvex négyszög átlóinak metszéspontja \(\displaystyle E\). Tegyük fel, hogy \(\displaystyle AB=CD\), és az \(\displaystyle ABE\) háromszög területe megegyezik a \(\displaystyle CDE\) háromszög területével. Mutassuk meg, hogy a négyszög paralelogramma vagy húrtrapéz.

Javasolta: Hujter Mihály (Budapest)

(3 pont)

A beküldési határidő 2025. december 10-én LEJÁRT.

Megoldás. A \(\displaystyle BCA\) és \(\displaystyle BCD\) háromszögek területe is egyenlő, hiszen a közös területrészt (\(\displaystyle BCE\) háromszög) elvéve belőlük éppen a \(\displaystyle ABE\) és \(\displaystyle CDE\) háromszögek maradnak, melyek területe a feladat feltételei szerint egyenlő.

Mivel a \(\displaystyle BCA\) és a \(\displaystyle BCD\) egyenlő területű háromszögek \(\displaystyle BC\) alapja közös, ezért \(\displaystyle A\) és \(\displaystyle D\) egyenlő távolságra kell legyen a \(\displaystyle BC\) egyenestől, méghozzá annak azonos oldalán (hiszen \(\displaystyle ABCD\) konvex). Tehát \(\displaystyle AD \parallel BC\), a négyszög trapéz.

Az pedig már közismert, hogy ha egy trapéz két szára egyenlő, akkor csak paralelogramma vagy húrtrapéz (szimmetrikus trapéz) lehet.

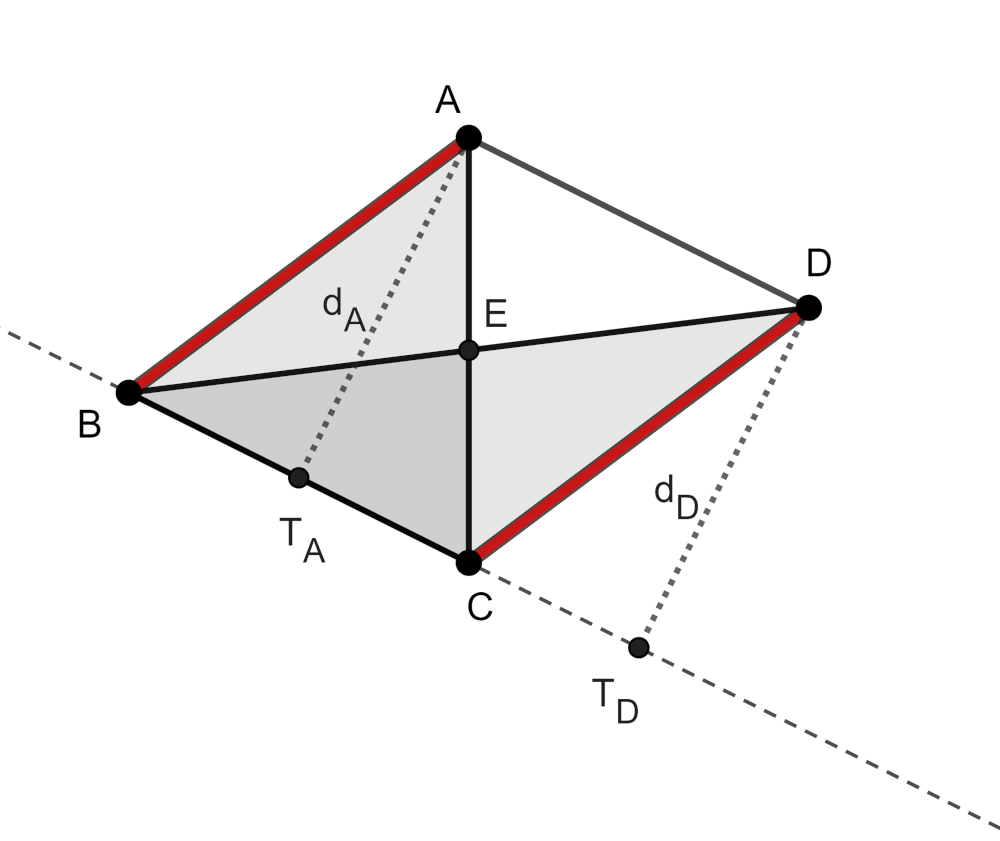
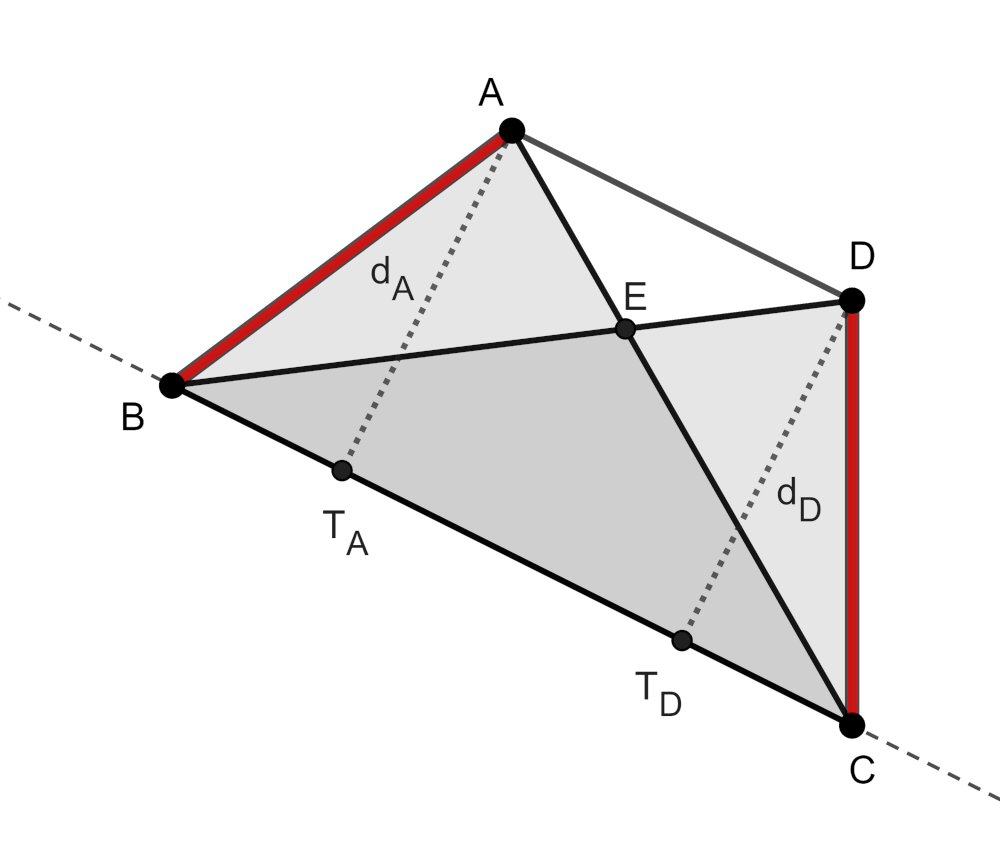
Megjegyzés. Ugyan közismertnek tekintjük (a versenyzőktől sem várjuk el a bizonyítás leírását), azért érdemes átismételni annak bizonyítását, hogy ha egy trapéz két szára egyenlő, akkor csak paralelogramma vagy húrtapéz lehet. Használjuk a feladat jelöléseit, legyen továbbá \(\displaystyle T_A\), ill. \(\displaystyle T_D\) az \(\displaystyle A\), ill. \(\displaystyle D\) pontból a \(\displaystyle BC\) egyenesre vett merőlegesek talppontja. Ekkor \(\displaystyle ABT_A\) és \(\displaystyle DCT_D\) egybevágó derékszögű háromszögek, hiszen \(\displaystyle AT_A\) és \(\displaystyle DT_D\) befogóik, illetve az átfogóik is egyeznek (,,két oldal és a nagyobbikkal szemközti szög'' egybevágósági alapeset).

• Ha \(\displaystyle ABT_A\) és \(\displaystyle DCT_D\) azonos körüljárású háromszögek, akkor a \(\displaystyle \overrightarrow{BC}\) vektorral való eltolás viszi előbbit utóbbiba. Így \(\displaystyle BA\) és \(\displaystyle CD\) is párhuzamos, a trapéz paralelogramma.
• Ha \(\displaystyle ABT_A\) és \(\displaystyle DCT_D\) ellentétes körüljárású háromszögek, akkor a \(\displaystyle BC\) felezőmerőlegesére való tengelyes tükrözés viszi előbbit utóbbiba. A \(\displaystyle BC\) felezőmerőlegese egyben a trapéz szimmetriatengelye is.

Statisztika:

A B. 5486. feladat értékelése még nem fejeződött be.

A KöMaL 2025. novemberi matematika feladatai