A B. 5488. feladat (2025. november)

B. 5488. Ki lehet-e színezni a sík minden pontját három szín egyikével úgy, hogy mindegyik színt felhasználjuk legalább egyszer, és ha egy háromszög minden csúcsa két szín egyikével van színezve, akkor azon háromszög minden belső-, és határpontja is ezen két szín valamelyikét viselje?

Javasolta: Lovas Márton (Budakalász)

(4 pont)

A beküldési határidő 2025. december 10-én LEJÁRT.

Megoldás. Legyen a három szín piros, kék és zöld. Megmutatjuk, hogy nem lehetséges a feladat feltételei szerint kiszínezni a síkot.

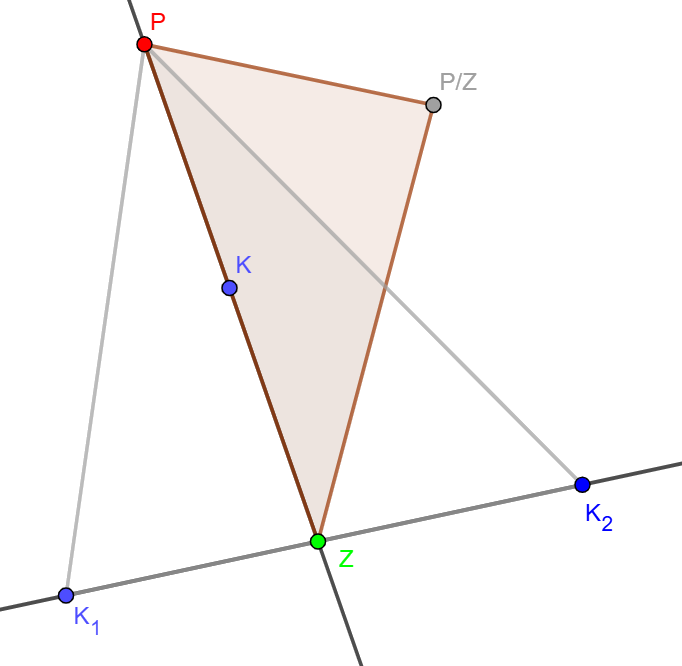
Először tegyük fel, hogy egy egyenesen találunk egy piros (\(\displaystyle P\)), egy kék (\(\displaystyle K\)) és egy zöld (\(\displaystyle Z\)) pontot (ebben a sorrendben). Ekkor az egyenesen kívül minden pont szükségképpen kék, különben az egyenesen lévő \(\displaystyle P\) és \(\displaystyle Z\) pontot kiegészítve egy az egyenesen kívüli nem kék ponttal olyan piros-zöld csúcsú háromszöget kapunk, amiben benne van \(\displaystyle K\) - ez ellentmond a feladat feltételeinek. Másrészről, ha minden pont kék az egyenesen kívül, akkor válasszunk két kék pontot (\(\displaystyle K_1\) és \(\displaystyle K_2\)) az egyenesen kívül, amik közrefogják \(\displaystyle Z\)-t. Ekkor \(\displaystyle K_1K_2P\) egy olyan piros-kék háromszög, amiben benne van \(\displaystyle Z\) - ismét ellentmondás. Kaptuk, hogy minden egyenesen legfeljebb kétféle színű pont lehet.

Most tegyük fel, hogy egy piros-kék egyenesen a \(\displaystyle P_1\) és \(\displaystyle P_2\) piros pont közrefogja a \(\displaystyle K\) kék pontot. A feltételek szerint van egy \(\displaystyle Z\) zöld pont (szükségképpen az előbbi egyenesen kívül), s így a \(\displaystyle ZP_1P_2\) háromszögben benne van \(\displaystyle K\), ellentmondás. Ezzel megmutattuk, hogy egy kétszínű egyenesen nem fordulhat elő, hogy két azonos színű pont közrefog egy tőlük különböző színűt. Ezt úgy is felfoghatjuk, hogy minden kétszínű egyenesen található egy pont, amelyhez tartozó egyik nyílt félegyenes az egyik színnel, a másik nyílt félegyenes a másik színnel van színezve (és maga a választópont is ezen két szín valamelyikét kapja).

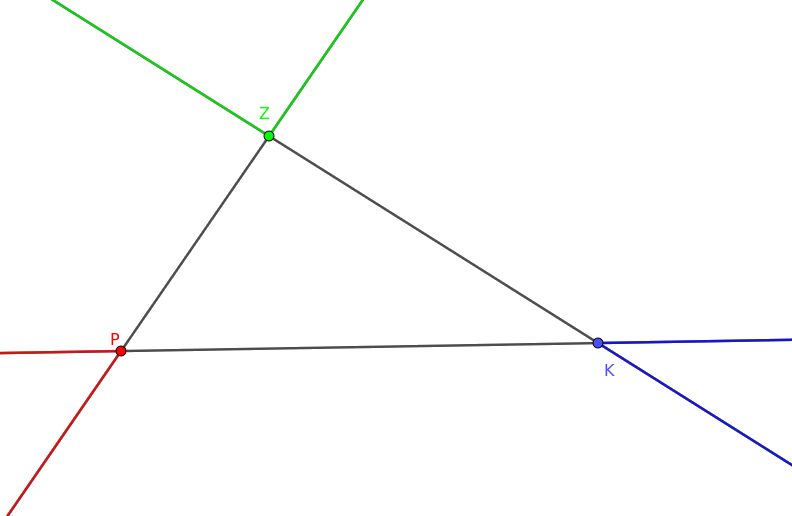
Tekintsünk most egy trikolor \(\displaystyle PKZ\) háromszöget. Az eddigiek szerint a \(\displaystyle PZ\) oldalegyenes \(\displaystyle Z\)-n túli félegyenese szükségképpen (teljesen) zöld, és hasonlót mondhatunk a többi öt, csúcson túli félegyenesről is, lásd az ábrát.

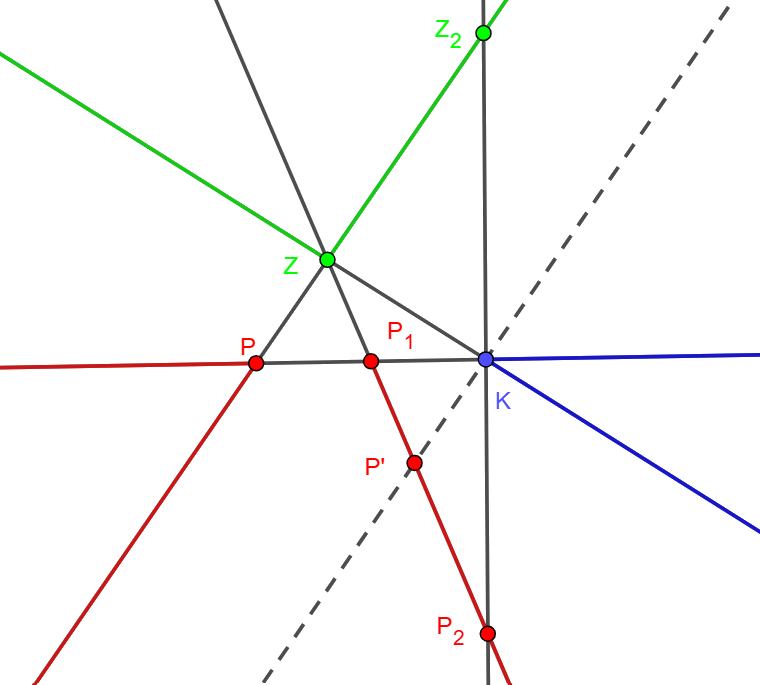
A \(\displaystyle PK\) oldal felezőpontjáról feltehetjük, hogy piros, jelölje ezt a pontot \(\displaystyle P_1\), ekkor \(\displaystyle ZP_1\) egyenes zöld és piros színű. A \(\displaystyle K\)-n keresztül húzzunk párhuzamost \(\displaystyle PZ\)-vel, ez messe a \(\displaystyle ZP_1\) egyenest egy \(\displaystyle P'\) pontban. Világos, hogy ekkor \(\displaystyle P_1\) a \(\displaystyle ZP'\) szakasz belsejében van. Vegyünk most fel egy \(\displaystyle P_2\) pontot a \(\displaystyle ZP'\) szakasz \(\displaystyle P'\)-n túli meghosszabbításán. Ekkor egyrészt \(\displaystyle P_2\) piros (mivel a zöld \(\displaystyle Z\)-től elválasztja a piros \(\displaystyle P_1\) a zöld-piros \(\displaystyle ZP_1\) egyenesen), másrészt \(\displaystyle P_2K\) a piros-zöld \(\displaystyle PZ\) egyenest a \(\displaystyle Z\) pontnak a \(\displaystyle P\)-vel ellentétes oldalán, tehát egy zöld színű \(\displaystyle Z_1\) pontban metszi. Így \(\displaystyle P_2\), \(\displaystyle K\) és \(\displaystyle Z_1\) három különböző színű pont egy egyenesen, ellentmondva a korábbi megállapításunknak. Ezzel beláttuk, hogy nem létezik megfelelő színezés.

Statisztika:

91 dolgozat érkezett.
4 pontot kapott:	Ali Richárd, Balla Ignác , Baranyi Ernő, Beinschroth Máté, Bodó Rókus Dániel, Bodor Ádám, Budai Máté, Chemlal Youva 118, Deák Boldizsár Tamás, Diaconescu Tashi, Ercse Ferenc, Gaál Gergely, Holló Martin, Kerekes András, Kiss Villő Zsófia, Kurucz Lilien Jázmin, Lazur András, Lovas Márk, Miszori Márton, Molnár Lili, Mura Liza Katalin, Nguyen Ngoc Mai, Pázmándi József Áron, Rajtik Sándor Barnabás, Rotter Szabolcs, Sajter Klaus, Sánta Gergely Péter, Sarusi-Kis Balázs, Sasvári Zoltán, Schmidt Botond, Szabó-Caceres Alan Martin, Taczman Vince, Tóth Luca, Vályi Nagy Ádám András, Varga 511 Vivien, Várhegyi Hanna, Varsányi Benedek, Weng Chenxin, Wiener Marcell, Zhai Yu Fan, Zhu Hongyu, Zhu Yi.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	14 versenyző.
1 pontot kapott:	13 versenyző.
0 pontot kapott:	8 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2025. novemberi matematika feladatai