 |
A B. 5489. feladat (2025. november) |
B. 5489. Az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle ABC\sphericalangle=15^\circ\) és \(\displaystyle CAB\sphericalangle=75^\circ\), továbbá az \(\displaystyle AB\) átfogó felezőpontja \(\displaystyle F\). A \(\displaystyle BC\) befogón vegyük fel a \(\displaystyle D\) pontot úgy, hogy \(\displaystyle BD=CA\), a \(\displaystyle CA\) félegyenesen az \(\displaystyle A\) ponton túl az \(\displaystyle E\) pontot úgy, hogy \(\displaystyle CE=BC\) teljesüljön. A \(\displaystyle BE\) és \(\displaystyle CF\) egyenesek metszéspontja legyen \(\displaystyle M\). Bizonyítsuk be, hogy a \(\displaystyle DM\) és \(\displaystyle CM\) egyenesek érintik az \(\displaystyle AEF\) háromszög köré írt kört.
Javasolta: Bíró Bálint (Eger)
(4 pont)
A beküldési határidő 2025. december 10-én LEJÁRT.
1. megoldás. Először a \(\displaystyle CM\) egyenesről mutatjuk meg, hogy érinti az \(\displaystyle AEF\) kört. A szövegben szereplő adatokon túl ábránkon vegyük fel az \(\displaystyle EB\) szakasznak azt a \(\displaystyle K\) pontját, amelyre \(\displaystyle FK=FB\), az \(\displaystyle AB\) átfogó fele.
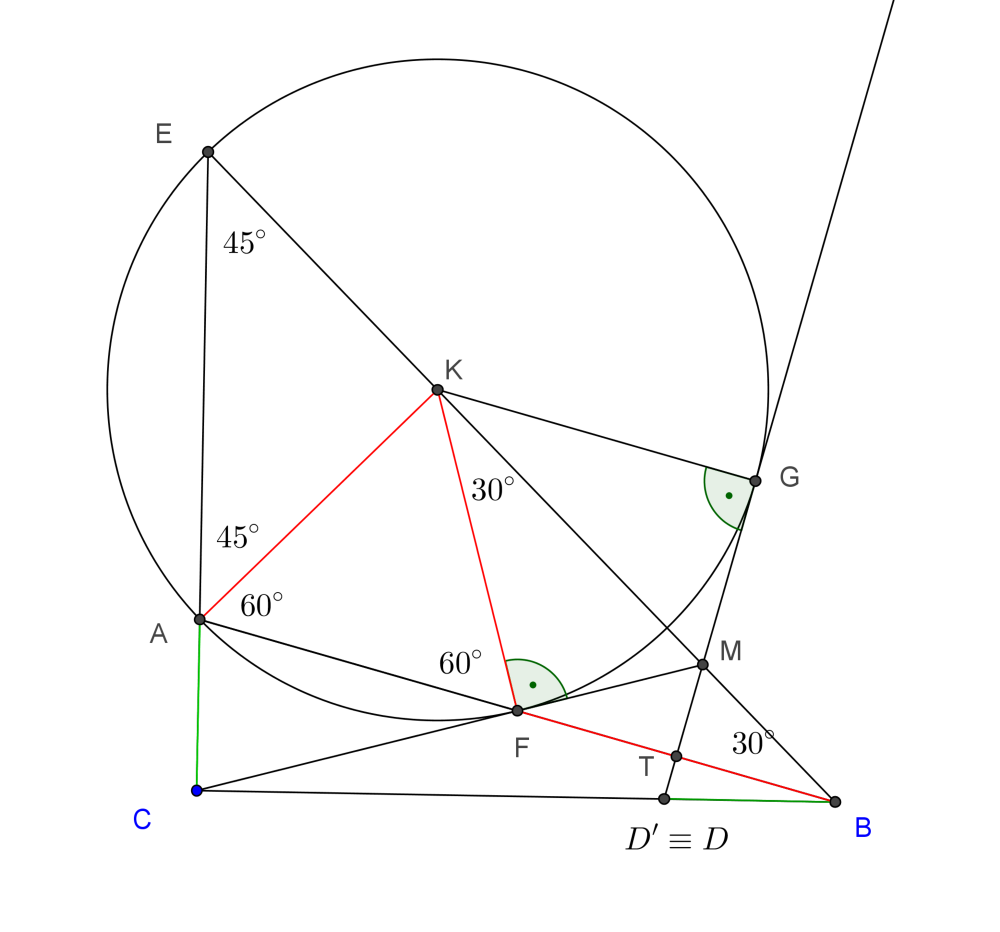
Az \(\displaystyle ECB\) háromszög egyenlő szárú derékszögű háromszög, így \(\displaystyle FBK\sphericalangle=30^\circ\). A \(\displaystyle K\) pont felvétele alapján \(\displaystyle FKB\sphericalangle\) is \(\displaystyle 30^\circ\), a \(\displaystyle KFB\) háromszög \(\displaystyle K\)-nál fekvő külső szöge pedig \(\displaystyle 60^\circ\), ezen kívül \(\displaystyle AF=FK\), vagyis \(\displaystyle AFK\) szabályos háromszög.
\(\displaystyle EAK\sphericalangle=EAB\sphericalangle- KAF\sphericalangle=105^\circ-60^\circ=45^\circ.\)
Ezzel már azt is látjuk, hogy \(\displaystyle AKE\) háromszög is egyenlő szárú, \(\displaystyle EAK\sphericalangle=AEK\sphericalangle=45^\circ\). Megmutattuk, hogy \(\displaystyle FK=AK=EK\), vagyis \(\displaystyle K\) pont az \(\displaystyle AEF\) kör középpontja.
Számoljuk ki most a \(\displaystyle CFK\) szöget! Az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle AF=FB=FC\), \(\displaystyle CFA\sphericalangle\) a \(\displaystyle CFB\) egyenlő szárú háromszög külső szöge, tehát \(\displaystyle CFA\sphericalangle=30^\circ\). Ha ehhez hozzávesszük, hogy \(\displaystyle AFK\sphericalangle=60^\circ\), akkor azonnal adódik, hogy az \(\displaystyle EAK\) kör \(\displaystyle KF\) sugara merőleges a \(\displaystyle CM\)-re, \(\displaystyle CM\) érintője a körnek. Itt azt az ismert tényt is kapjuk, hogy az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-hez tartozó magassága \(\displaystyle \frac{c}{4}\), lévén \(\displaystyle CFA\sphericalangle=30^\circ\), az ezzel szemközti befogó az átfogó (most \(\displaystyle \frac{c}{2}\)) fele.
A másik érintés bizonyításához tükrözzük a \(\displaystyle CM\) érintőt az \(\displaystyle EM\) egyenesre. Legyen az \(\displaystyle F\) pont tükörképe \(\displaystyle G\). Messe a \(\displaystyle GM\) érintő egyenese az \(\displaystyle AB\) átfogót a \(\displaystyle T\), a \(\displaystyle CB\) befogót a \(\displaystyle D'\) pontban. Azt fogjuk megmutatni, hogy a \(\displaystyle D\) és \(\displaystyle D'\) pontok egybeesnek.
Az első részben láttuk, hogy \(\displaystyle FKM\sphericalangle=30^\circ\), a \(\displaystyle KFM\) derékszögű háromszög félszabályos. A tükrözés után \(\displaystyle KMG\sphericalangle\) és csúcsszöge \(\displaystyle TMB\sphericalangle\) \(\displaystyle 60^\circ\)-osak, \(\displaystyle MTB\) derékszög, \(\displaystyle T\) pont felezi az \(\displaystyle FB\) szakaszt.
A \(\displaystyle BD'T\) derékszögű háromszög hasonló az eredeti \(\displaystyle BAC\) háromszöghöz, mert \(\displaystyle B\)-nél közös hegyesszögük van. Számítsuk ki az \(\displaystyle x=BD'\) szakasz hosszát a hasonlóság alapján:
\(\displaystyle x:c=\frac{c}{4}: a, \qquad xa=\frac{c^2}{4}.\)
Az első részben rögzítettük, hogy az \(\displaystyle ABC\) háromszög átfogóhoz tartozó magassága éppen \(\displaystyle \frac{c}{4}\), így \(\displaystyle \frac{c^2}{4}\) a kétszeres terület, vagyis a befogók szorzatával összevetve \(\displaystyle x=b\). A \(\displaystyle D'\) pont valóban egybeesik a \(\displaystyle D\) ponttal, \(\displaystyle DM\) az \(\displaystyle AEF\) kör érintője.
2. megoldás. A megoldás első lépése a \(\displaystyle D\) pont konstrukciójának megértése. Vegyük fel sorban azokat a \(\displaystyle P\in AB\), \(\displaystyle Q\in BC\), \(\displaystyle R\in BP\), majd \(\displaystyle S\in BQ\) pontokat, amelyekre \(\displaystyle AC=CP=PQ=QR=RS\). A \(\displaystyle CPA\), \(\displaystyle PCQ\), \(\displaystyle QRP\) és \(\displaystyle RQS\) egyenlő szárú háromszögek szögeinek összeszámolásából kapjuk az ábrán megjelölt szögeket:
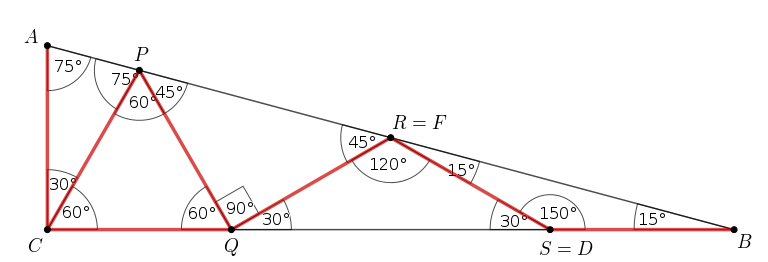
A \(\displaystyle CQP\) háromszög szabályos, mert mindegyik szöge \(\displaystyle 60^\circ\), továbbá a \(\displaystyle BRS\) háromszög is egyenlő szárú, mert \(\displaystyle RBS\sphericalangle=15^\circ=SRB\sphericalangle\). Ezért a \(\displaystyle CQ=CP\) és a \(\displaystyle BS=RS\). A \(\displaystyle CQR\) és az \(\displaystyle RSB\) egyenlő szárú háromszögek egybevágók, mert szögeik és és száraik megegyeznek. Ezekből leolvashatjuk, hogy \(\displaystyle S=D\) és \(\displaystyle R=F\).
Ezek után egészítsük ki a \(\displaystyle CBE\) háromszöget a \(\displaystyle CBGE\) négyzetté, és legyen \(\displaystyle H\in BG\) és \(\displaystyle I\in EG\) az a két pont, amelyre \(\displaystyle BH=GI=AC\).
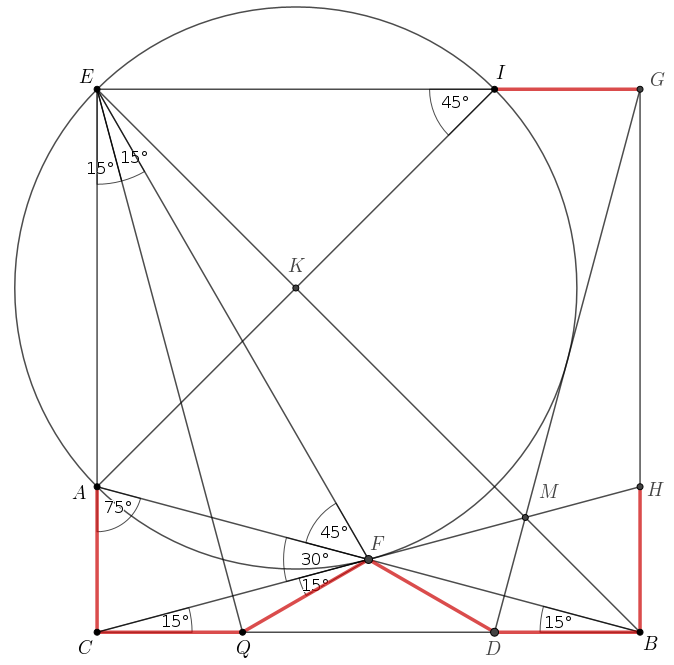
A \(\displaystyle CQE\) és a \(\displaystyle BHC\) háromszögek egymás \(\displaystyle 90^\circ\)-os elforgatottjai (az elforgatás középpontja a \(\displaystyle BE\) szakasz felezőpontja), ezért \(\displaystyle EQ\perp CF\). Mivel a \(\displaystyle CQF\) háromszög egyenlő szárú, ez azt jelenti, hogy \(\displaystyle EQ\) a \(\displaystyle CF\) szakasz felezőmerőlegese, ezért a \(\displaystyle CQFE\) négyszög deltoid. A deltoid és a \(\displaystyle CBF\) háromszög szögeinek összeszámolásából \(\displaystyle AEF\sphericalangle=30^\circ=AFC\sphericalangle\), \(\displaystyle EFA\sphericalangle=45^\circ=EIA\sphericalangle\). Utóbbi miatt az \(\displaystyle AFE\) kör átmegy az \(\displaystyle I\) ponton, és a kör \(\displaystyle K\) középpontja az \(\displaystyle AIE\) egyenlő szárú derékszögű háromszög \(\displaystyle AI\) átfogójának felezőpontja; a kör szimmetrikus az \(\displaystyle AI\) húr felező merőlegesére, ami a négyzet \(\displaystyle BE\) átlója.
Végül, \(\displaystyle AFC\sphericalangle=AEF\sphericalangle\) miatt a \(\displaystyle CFM\) egyenes érinti az \(\displaystyle AFE\) kört. A \(\displaystyle GMD\) egyenes a \(\displaystyle CFM\) érintő tükörképe a kör középpontján átmenő \(\displaystyle KM\)-re, ezért ez is érinti a kört.
Statisztika:
71 dolgozat érkezett. 4 pontot kapott: Ali Richárd, Antal Tamás Botond, Balla Ignác , Bao Nguyen Gia, Blaskovics Ádám, Bodó Rókus Dániel, Bodor Ádám, Diaconescu Tashi, Ercse Ferenc, Hajba Milán, Hideg János, Holló Martin, Illés Dóra, Kerekes András, Kiss Villő Zsófia, Kővágó Edit Gréta, Kurucz Lilien Jázmin, Li Mingdao, Lovas Márk, Maróti Olga, Molnár-Sáska Tamás, Nagypál Katóca, Pázmándi József Áron, Péter Hanna, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Sasvári Zoltán, Takács András, Tarján Emma, Tóth Luca, Varga 511 Vivien, Várhegyi Hanna, Weng Chenxin, Wiener Marcell, Zhai Yu Fan, Zhu Yi. 3 pontot kapott: Fodor Barna, Mikó Hédi Irma, Miszori Márton, Molnár Lili, Sógor-Jász Soma. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2025. novemberi matematika feladatai

