 |
A B. 5493. feladat (2025. november) |
B. 5493. Írjunk fel olyan, a síkvektorokhoz nemnegatív számokat rendelő \(\displaystyle f\) függvényt, amelyre teljesül, hogy bármely, az \(\displaystyle x^2-y^2=1\) hiperbolába írt \(\displaystyle ABC\) háromszög területe \(\displaystyle f\Big(\overrightarrow{AB}\Big)\cdot f\Big(\overrightarrow{BC}\Big)\cdot f\Big(\overrightarrow{CA}\Big)\).
Javasolta: Kós Géza (Budapest)
(6 pont)
A beküldési határidő 2025. december 10-én LEJÁRT.
Megoldás. Az egyszerűbb számolás kedvéért forgassuk el a koordináta-rendszerünket \(\displaystyle -45\) fokkal. Az új koordináta-rendszerben a koordinátákat jelölje \(\displaystyle x'\) és \(\displaystyle y'\); az \(\displaystyle x'\)-tengely éppen az \(\displaystyle y=-x\) egyenes, az \(\displaystyle y'\)-tengely pedig az \(\displaystyle y=x\) egyenes lesz. Az \(\displaystyle (x,y)\) pont koordinátái az új koordináta-rendszerben \(\displaystyle (x',y')=((x-y)/\sqrt 2, (x+y)/\sqrt 2)\). Fordítva kifejezve: \(\displaystyle (x,y)=((x'+y')/\sqrt 2, (x'-y')/\sqrt 2)\).
Utóbbit visszaírva a hiperbola egyenletébe kapjuk, hogy
\(\displaystyle 1=x^2-y^2=((x'+y')/\sqrt 2)^2-((x'-y')/\sqrt 2)^2=2x'y';\)
azaz az új koordináta-rendszerben a hiperbola egyenlete \(\displaystyle x'y'=1/2.\)
Felhasználjuk a következő, ismert képletet. (Lásd pl. a Wikipédián.) Az \(\displaystyle A(x_A, y_A)\), \(\displaystyle B(x_B,y_B)\), \(\displaystyle C(x_C,y_C)\) pontok által adott háromszög területe
\(\displaystyle T_{ABC}=\frac 12 \left |\det \left ( \begin{matrix} x_A & y_A & 1\\ x_B & y_B & 1\\ x_C & y_C & 1 \end{matrix} \right ) \right |=\frac 12 \left | x_Ay_B-x_Ay_C+x_By_C-x_By_A+x_Cy_A-x_Cy_B \right |.\)
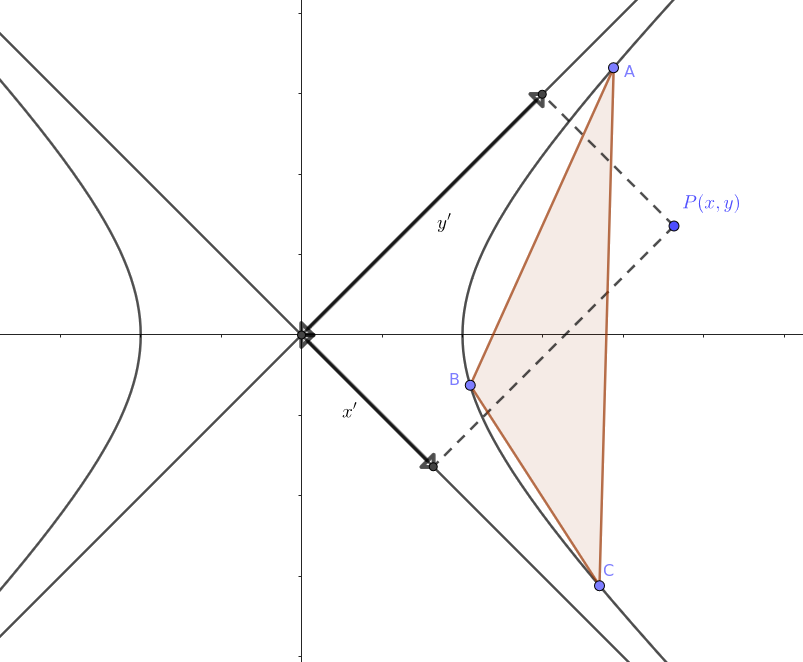
Számítsuk ki ezzel \(\displaystyle A(a,1/2a)\), \(\displaystyle B(b, 1/2b)\), \(\displaystyle C(c,1/2c)\), a hiperbolába írt háromszög területét.
\(\displaystyle T_{ABC}=\frac 14 \left |\frac ab - \frac ba+ \frac bc -\frac cb +\frac ca - \frac ac \right | \)
adódik, ahol az abszolút értékből az \(\displaystyle 1/2\)-t már kiemeltük. Közös nevezőre hozás után észrevehetjük, hogy a számláló szorzattá alakul, így kapjuk a következő (kiszorzással közvetlenül ellenőrizhető) formulát:
\(\displaystyle T_{ABC}=\frac 14 \left |\frac ab - \frac ba+ \frac bc -\frac cb +\frac ca - \frac ac \right |=\frac 14 \left | \frac{(a-b)(b-c)(c-a)}{abc}\right |. \)
Vegyük észre, hogy \(\displaystyle \overrightarrow{AB}=(b-a,1/2b-1/2a)=(b-a,(a-b)/2ab).\) Így a \(\displaystyle \hat f(x',y')=\sqrt{|x'y'|}/\sqrt[6] 2\) függvény az \(\displaystyle \overrightarrow{AB}\)-hoz épp
\(\displaystyle \hat f(\overrightarrow {AB})=\hat f\left(b-a,\frac{a-b}{2ab} \right )=\frac{1}{\sqrt[6] 2}\cdot \sqrt{\left | (b-a)\cdot \frac {a-b}{2ab} \right |}=\frac1{\sqrt[6] 2 \cdot \sqrt 2} \cdot \frac{|a-b|}{\sqrt{|ab|}}=\frac1{\sqrt[3] 4} \frac{|a-b|}{\sqrt{|ab|}}\)
értéket rendeli. Hasonlóan kifejezve \(\displaystyle \hat f\) értékét a \(\displaystyle \overrightarrow {BC}\) és \(\displaystyle \overrightarrow {CA}\) vektorok esetén kapjuk, hogy
\(\displaystyle \hat f(\overrightarrow {AB}) \cdot \hat f(\overrightarrow {BC}) \cdot \hat f(\overrightarrow {CA})=T_{ABC}.\)
Visszatérve az eredeti \(\displaystyle xy\)-koordinátáinkra az eddigiekből kapjuk, hogy \(\displaystyle \vec v=(x,y)\)-hoz
\(\displaystyle f(\vec v)=f(x,y)=\hat f(x',y')=\frac{\sqrt{|x'y'|}}{\sqrt[6] 2}=\frac{\sqrt{\left | \frac{x-y}{\sqrt 2} \cdot \frac{x+y}{\sqrt 2}\right |}}{\sqrt[6] 2}=\frac{\sqrt{|x^2-y^2|}}{\sqrt[3] 4}\)
értéket rendelő \(\displaystyle f\) függvény megfelelő. Ezzel a feladatot megoldottuk.
Megjegyzés. Lényegében ugyanígy végigszámolható a feladata az \(\displaystyle xy\)-koordinátákat használva is, de a kapott formulák kellemetlenebbek.
Statisztika:
A B. 5493. feladat értékelése még nem fejeződött be.
A KöMaL 2025. novemberi matematika feladatai