Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 1090. feladat (2011. október)

C. 1090. Tizenhárom szabályos dobókockából összeragasztottuk a képen látható testet. Hány pötty lehet maximálisan a felületén?

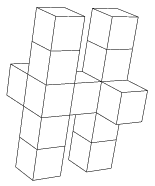
(5 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldás. Egy szabályos dobókocka tetszőleges szemközti oldalpárján összesen 7 pötty van (egy kockán összesen 21): azokat a kockákat kel ügyesen ragasztani, melyekcsak 1 oldalukkal vagy 2 egymás mellettival kapcsolódnak a többihez. Ekkor az 1 pötty illetve 1 és 2 pöttyös felet kell a szomszédhoz illeszteni. Ha két szemközti oldalával kapcsolódik egy kocka a többihez, akkor mindegy, melyik oldalpár nem látszik, minden

kockák száma kívül levő pöttyök kockánként összesen
6 1-est ragaszt - 20 pötty 120
2 1-est és 2-est ragaszt - 18 pötty 36
5 két szemközti oldalukkal csatlakoznak - 14 pötty 70

Összesen \(\displaystyle 120+36+70=226\) pöttyöt lehet legfeljebb látni.

Statisztika:

559 dolgozat érkezett.
5 pontot kapott:443 versenyző.
4 pontot kapott:53 versenyző.
3 pontot kapott:34 versenyző.
2 pontot kapott:12 versenyző.
1 pontot kapott:4 versenyző.
0 pontot kapott:7 versenyző.
Nem versenyszerű:6 dolgozat.

A KöMaL 2011. októberi matematika feladatai