 |
A C. 1093. feladat (2011. október) |
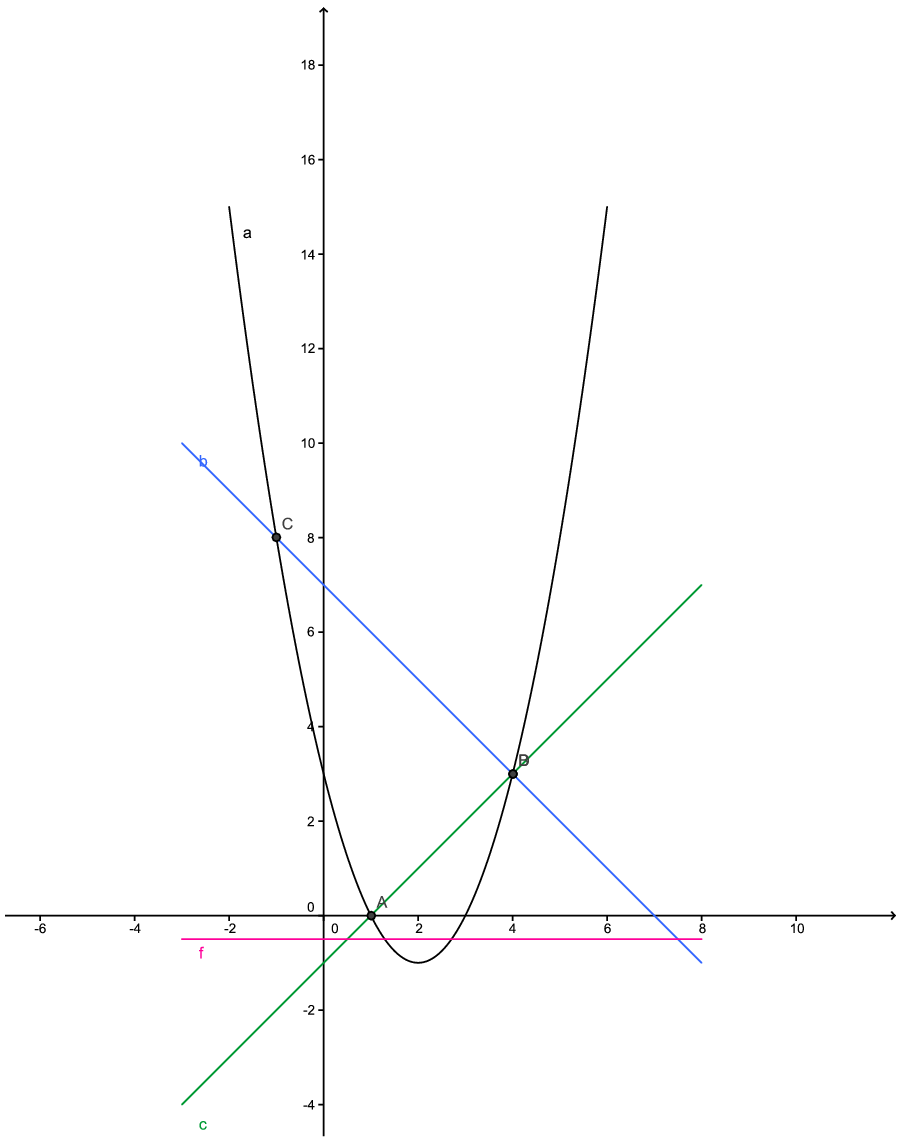
C. 1093. Az f(x) függvény helyettesítési értéke tetszőleges x valós szám esetén legyen az x2-4x+3, az x-1 és a -x+7 értékek közül a legkisebb. Adjuk meg az f(x)=c egyenlet megoldásainak számát a c valós paramétertől függően.
(5 pont)
A beküldési határidő 2011. november 10-én LEJÁRT.
Megoldás. \(\displaystyle x^4x+3=x-1\) akkor, ha \(\displaystyle x=0\) vagy \(\displaystyle x=4\), ugyanakkor \(\displaystyle x^4x+3=-x+7\) akkor, ha \(\displaystyle x=-1\) vagy \(\displaystyle x=4\). Ekkor az \(\displaystyle f(x)\) a következő: ha \(\displaystyle x<1\), akkor \(\displaystyle x-1\); ha \(\displaystyle 1\le x<4\), akkor \(\displaystyle x^2-4x+3\); ha \(\displaystyle 4\le x\), akkor \(\displaystyle -x+7\).
|
A megoldások száma:
|
Statisztika:
292 dolgozat érkezett. 5 pontot kapott: 196 versenyző. 4 pontot kapott: 27 versenyző. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 41 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2011. októberi matematika feladatai
