A C. 1148. feladat (2012. december)

C. 1148. Egy körbe írt négyszög átlói merőlegesek egymásra. Bizonyítsuk be, hogy bármelyik oldalának távolsága a kör középpontjától egyenlő a szemben lévő oldal felével.

Kvant

(5 pont)

A beküldési határidő 2013. január 10-én LEJÁRT.

Megoldás. Készítsünk ábrát.

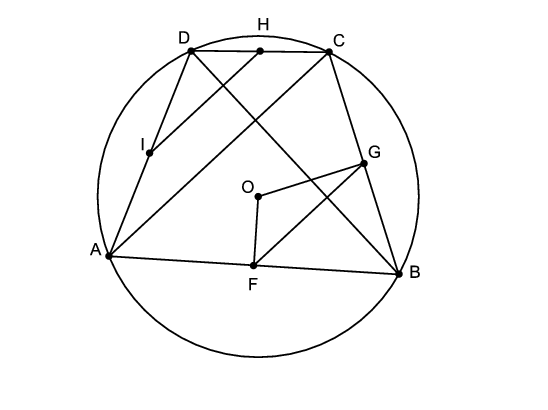
Kössük össze egymással az \(\displaystyle F\), \(\displaystyle G\) és \(\displaystyle H\), \(\displaystyle I\) oldalfelező pontokat. Az \(\displaystyle FG\), illetve \(\displaystyle HI\) szakaszok az \(\displaystyle ABC\), illetve az \(\displaystyle ACD\) részháromszögekben középvonalak, így az \(\displaystyle AC\) átló felével, és így egymással is egyenlők.

Könnyen belátható, hogy \(\displaystyle DIH\angle=DAC\angle=OGF\angle\), illetve \(\displaystyle DHI\angle=DCA\angle=OFG\angle\):

\(\displaystyle DIH\angle=DAC\angle\) és \(\displaystyle DHI\angle=DCA\angle\), mert egyállású szögek. \(\displaystyle DAC\angle=DBC\angle\) a kerületi szögek tétele miatt, \(\displaystyle DBC\angle=OGF\angle\), mert merőleges szárú szögek (hiszen \(\displaystyle FG\parallel AC\), és \(\displaystyle AC\perp DB\), illetve egy kör középpontját egy húr felezőpontjával összekötő szakasz merőleges a húrra). Hasonlóan \(\displaystyle DCA\angle=DBA\angle\) és \(\displaystyle DBA\angle=OFG\angle\).

Ezekből már következik, hogy az \(\displaystyle OFG\triangle\) és a \(\displaystyle DHI\triangle\) egybevágó, tehát \(\displaystyle OF=DH=\frac{DC}{2}\).

A másik három oldalra ugyanígy lehet belátni az állítást.

Statisztika:

169 dolgozat érkezett.
5 pontot kapott:	127 versenyző.
4 pontot kapott:	6 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	22 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2012. decemberi matematika feladatai