A C. 1152. feladat (2013. január)

C. 1152. Legyen

és

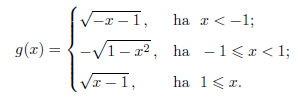
Adjuk meg f-g zérushelyeit.

(5 pont)

A beküldési határidő 2013. február 11-én LEJÁRT.

Megoldás. I.) Ha \(\displaystyle x\geq -3/2\), akkor \(\displaystyle f(x)=x+3/2-3/2=x\). Ekkor 3 eset van.

1.) \(\displaystyle -3/2\leq x<-1\). Ekkor az egyenlet:

\(\displaystyle x=\sqrt{-x-1}.\)

A bal oldal negatív, a jobb oldal nem, ezért nincs megoldás.

2.) \(\displaystyle -1\leq x<1\). Ekkor az egyenlet:

\(\displaystyle x=-\sqrt{1-x^2}.\)

Mivel a jobb oldal legfeljebb 0, ezért \(\displaystyle -1\leq x\leq0\). Négyzetre emelve, majd rendezve:

\(\displaystyle x^2=1-x^2,\)

\(\displaystyle 2x^2-1=0.\)

Ennek megoldása \(\displaystyle \pm\sqrt2/2\), ebből csak az egyik nem pozitív: \(\displaystyle x_1=-\sqrt2/2\).

3.) \(\displaystyle x\geq1\). Az egyenlet: \(\displaystyle x=\sqrt{x-1}\). Négyzetre emelve: \(\displaystyle x^2=x-1\), amiből \(\displaystyle 0=x^2-x+1=(x-1/2)^2+3/4\), ami lehetetlen.

II.) Ha \(\displaystyle x<-3/2\), akkor \(\displaystyle f(x)=-x-3/2-3/2=-x-3\). Ekkor az egyenlet:

\(\displaystyle -x-3=\sqrt{-x-1}.\)

Négyzetre emelve és rendezve:

\(\displaystyle x^2+6x+9=-x-1,\)

\(\displaystyle x^2+7x+10=(x+2)(x+5)=0.\)

A két gyök közül csak az egyik kisebb -3/2-nél: \(\displaystyle x_2=-5\).

Statisztika:

240 dolgozat érkezett.
5 pontot kapott:	119 versenyző.
4 pontot kapott:	77 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	14 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2013. januári matematika feladatai