A C. 1153. feladat (2013. január)

C. 1153. Egy egységnyi átlójú négyzetet egyik átlója mentén elvágunk, majd a másik átló egyenese mentén a két részt egymás felé toljuk. Legfeljebb mekkora területű közös rész jöhet létre?

(5 pont)

A beküldési határidő 2013. február 11-én LEJÁRT.

Megoldás. Egy egységnyi átlójú négyzet területe 1/2. Az \(\displaystyle ABCD\) négyzetet a \(\displaystyle BD\) átlója mentén kettévágva, az \(\displaystyle ABD\) háromszöget az \(\displaystyle A'B'D'\) háromszögbe toljuk el. Jelölje a \(\displaystyle DE\) szakasz hosszát \(\displaystyle y>0\). Ha \(\displaystyle y=DC/2\), akkor a közös rész pont a négyzet negyede, vagyis területe \(\displaystyle 1/8\). Ha még tovább toljuk a háromszöget, vagyis \(\displaystyle y>DC/2\), akkor a közös rész területe ennél kisebb lesz. Legyen \(\displaystyle y<DC/2\).

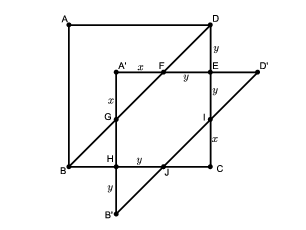
Az eltolás miatt ekkor \(\displaystyle HB'=DE=y\). Mivel a \(\displaystyle DEF\) és a \(\displaystyle HB'J\) háromszögek derékszögűek, és két másik szögük \(\displaystyle 45^{\circ}\)-os, ezért egyenlő szárúak, és így \(\displaystyle EF=HJ=y\). A szimmetria miatt ekkor \(\displaystyle EI=HJ=y\). Az \(\displaystyle AC\)-re való szimmetria miatt ekkor \(\displaystyle EI=HJ=y\) és \(\displaystyle GH=FE=y\).

Legyen az \(\displaystyle A'F\) szakasz hossza \(\displaystyle x\). Ekkor a fentiekhez hasonlóan \(\displaystyle A'G=x\) is teljesül. Vagyis \(\displaystyle A'B'=x+y+y=x+2y\). Mivel \(\displaystyle A'B'=DC\), így \(\displaystyle DC=x+2y\), amiből \(\displaystyle IC=x\).

Most már felírhatjuk a kérdéses területet. Ehhez felhasználjuk, hogy a négyzet oldalának hossza \(\displaystyle \frac{\sqrt2}{2}=x+2y\), amiből \(\displaystyle y=\frac{\sqrt2}{4}-\frac x2\).

\(\displaystyle t=t_{BCD}-t_{IJC}-2\cdot t_{DEF}=\frac14-\frac{x^2}{2}-2\cdot\frac{y^2}{2}=\)

\(\displaystyle =\frac14-\frac{x^2}{2}-\left(\frac{\sqrt2}{4}-\frac x2\right)^2=-\frac34x^2+\frac{\sqrt2}{4}x+\frac18=\)

\(\displaystyle =-\frac34\left(\left(x-\frac{\sqrt2}{6}\right)^2-\frac{8}{36}\right).\)

Tehát a terület \(\displaystyle x=\frac{\sqrt2}{6}\) esetén lesz a legnagyobb, értéke ekkor \(\displaystyle -\frac34\cdot\left(-\frac{8}{36}\right)=\frac16\).

Statisztika:

178 dolgozat érkezett.
5 pontot kapott:	92 versenyző.
4 pontot kapott:	29 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	18 versenyző.
0 pontot kapott:	20 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2013. januári matematika feladatai