Problem C. 1207. (January 2014)

C. 1207. E, F and G are points on each side of triangle ABC and n is a natural number such that $\frac{AE}{EB}=\frac{1}{n-1}$ , $\frac{BF}{FC}=\frac{1}{n}$ , and $\frac{CG}{GA}=\frac{1}{n+1}$ . Show that if n $\ge$ 5 then the area of triangle EFG is greater than the half of the area of triangle ABC.

(5 pont)

Deadline expired on February 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Számoljuk ki a három "levágott" háromszög területét. Elég azt belátni, hogy ezek területének összege n $\geq$ 5 esetén kisebb, mint az ABC háromszög területének a fele.

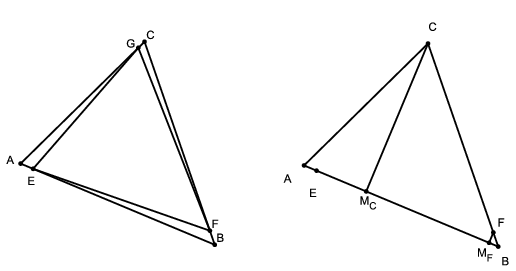
Mivel $\frac{AE}{EB}=\frac{1}{n-1}$ , ezért EB=(n-1)^.AE, és így AB=AE+(n-1)^.AE=n^.AE. Ebből pedig $EB=\frac{n-1}{n}\cdot AB$ .

Legyen CM_C az ABC háromszög C csúcsához tartozó magassága, FM_F pedig az EBF háromszög F csúcsához tartozó magassága. A párhuzamos szelők tétele miatt $\frac{M_FF}{M_CC}=\frac{BF}{BC}$ . Tudjuk, hogy $\frac{BF}{FC}=\frac1n$ , amiből a fentihez hasonló módon $\frac{BF}{BC}=\frac{1}{n+1}$ , tehát $\frac{M_FF}{M_CC}=\frac{1}{n+1}$ , amiből $M_FF=\frac{1}{n+1}\cdot M_CC$ . Ebből már számolható az EFB háromszög területe: $t_{EFB}=\frac12EB\cdot FM_F=\frac12\cdot\frac{n-1}{n}\cdot AB\cdot\frac{1}{n+1}\cdot M_CC=\frac12\cdot AB\cdot M_CC\cdot\frac{n-1}{n}\cdot\frac{1}{n+1}=t_{ABC}\cdot\frac{n-1}{n}\cdot\frac{1}{n+1}$ .

Hasonlóan $t_{FCG}=t_{ABC}\cdot\frac{n}{n+1}\cdot\frac{1}{n+2}$ és $t_{GAE}=t_{ABC}\cdot\frac{n+1}{n+2}\cdot\frac{1}{n}$ .

Tehát azt szeretnénk belátni, hogy

$\frac12\cdot t_{ABC}>t_{ABC}\cdot\frac{n-1}{n}\cdot\frac{1}{n+1}+t_{ABC}\cdot\frac{n}{n+1}\cdot\frac{1}{n+2} +t_{ABC}\cdot\frac{n+1}{n+2}\cdot\frac{1}{n}.$

Osztva t_ABC $\neq$ 0-val és a kifejezést alakítva:

$\frac12>\frac{n-1}{n}\cdot\frac{1}{n+1}+\frac{n}{n+1}\cdot\frac{1}{n+2} +\frac{n+1}{n+2}\cdot\frac{1}{n}=\frac{(n-1)(n+2)+n^2+(n+1)^2}{n(n+1)(n+2)}=$

$=\frac{3n^2+3n-1}{n(n+1)(n+2)}.$

Szorozva mindkét oldalt (2n(n+1)(n+2))>0-val:

n(n+1)(n+2)>6n²+6n-2,

n³+3n²+2n>6n²+6n-2,

n³-3n²-4n+2>0,

n(n²-3n-4)+2>0,

n(n+1)(n-4)+2>0.

Ez pedig nyilván teljesül, ha n $\geq$ 5, hiszen három pozitív szám szorzata pozitív, tehát a bal oldal 2-nél is nagyobb. A műveletek ekvivalensek voltak, tehát az állítás igaz.

Statistics:

88 students sent a solution.

5 points: Balázs Ákos Miklós, Bekő Mária, Bekő Zsófia, Bereczki Zoltán, Bottlik Judit, Demeter Dániel, Eper Miklós, Farkas Dóra, Fényes Balázs, Gáspár Attila, Horváth 016 Gábor, Kasó Ferenc, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kovács Péter Tamás, Matusek Márton, Mihálykó Péter, Molnár-Sáska Zoltán, Pap-Takács Mónika, Papp 535 Ágnes, Porupsánszki István, Regős Krisztina, Sebastian Fodor, Szabó 157 Dániel, Szabó 524 Tímea, Széles Katalin, Sziegl Benedek, Tóth Zsófia, Zsakó Ágnes, Zsiros Ádám.

4 points: 26 students.

3 points: 10 students.

2 points: 1 student.

1 point: 5 students.

0 point: 5 students.

Unfair, not evaluated: 10 solutionss.

Problems in Mathematics of KöMaL, January 2014

88 students sent a solution.
5 points:	Balázs Ákos Miklós, Bekő Mária, Bekő Zsófia, Bereczki Zoltán, Bottlik Judit, Demeter Dániel, Eper Miklós, Farkas Dóra, Fényes Balázs, Gáspár Attila, Horváth 016 Gábor, Kasó Ferenc, Kerekes Anna, Klász Viktória, Kocsis Júlia, Kovács Péter Tamás, Matusek Márton, Mihálykó Péter, Molnár-Sáska Zoltán, Pap-Takács Mónika, Papp 535 Ágnes, Porupsánszki István, Regős Krisztina, Sebastian Fodor, Szabó 157 Dániel, Szabó 524 Tímea, Széles Katalin, Sziegl Benedek, Tóth Zsófia, Zsakó Ágnes, Zsiros Ádám.
4 points:	26 students.
3 points:	10 students.
2 points:	1 student.
1 point:	5 students.
0 point:	5 students.
Unfair, not evaluated:	10 solutionss.

Already signed up?
New to KöMaL?